The vestiges of the Roman Empire continue to evoke wonder. Remnants from this era have been extensively documented and, although exhaustively studied, questions still abound surrounding many aspects of daily life in those days. One of the most curious is why, especially during the early imperial period, the Romans used asymmetrical dice.
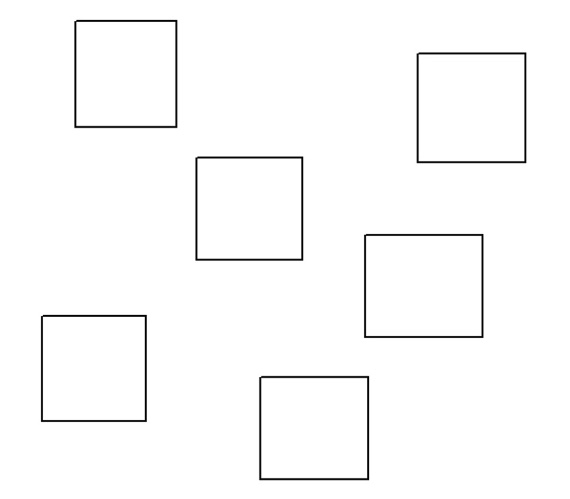
Brainteaser 1: Asymmetric shapes
The human eye is able to distinguish the difference in size between two objects (e.g. two stripes or edges) when the variation between them is 5% or more. This is the case for the edges of the asymmetric shapes included in this challenge and that you should therefore be able to distinguish: which ones are not square?
Hypotheses for all tastes
The propensity to use these unique lopsided cubic pieces has generated various hypotheses, although historians and anthropologists have settled on three main ones:
- The cultural hypothesis argues that the taste for lopsided dice would be a form of tradition or cultural heritage from pre-Roman times, a way of honouring and remembering the peoples who preceded the Romans, their ancestors.
- The unintentional or technical hypothesis states that the prevalence of asymmetrical dice in this period would be a consequence of both the limitations imposed by the materials used for their manufacture—usually bone, wood, metal or clay—and the lack of skill or practice of the craftsmen. This explanation is difficult to support since, on the one hand, these limitations are not observed in other pieces and objects made with the same materials, and on the other, because there are also symmetrical dice dating from the same period.
- Finally, there is the intentional or probabilistic hypothesis—the most widely accepted—which explains that the asymmetry was not only intentional and sought after, but that it had a specific function: that of favouring certain rolls or values (and specifically the 6), an important aspect in divinatory practices based on the throwing of dice and also in gambling. This argument is supported both by mathematical models and experimental probabilistic studies that show that the lopsided configuration favours the probability of the values of the faces with the largest surface area—the greater the ratio between the largest axis and the other two equal axes, the more likely it is.
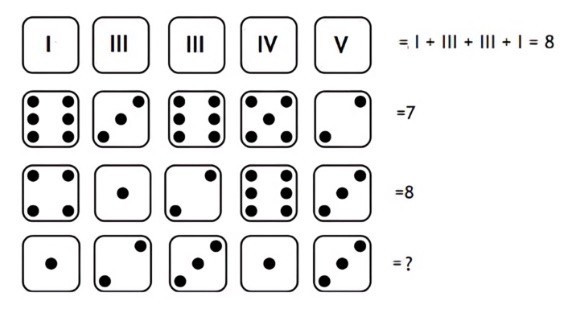
Brainteaser 2: Roman ones
One of the most popular dice-based logic problems is known as “polar bears hunt seals” (or alternatively “petals around roses“). Here we present a Roman variant. The challenge is to find out what the response of a citizen of the Roman Empire would be.

A new study, a new approach
A recent study offers a new approach to this Roman predilection for asymmetrical dice. To validate the probabilistic hypothesis, the researchers required a group of volunteers uninformed about the object of the experiment to label with dots replicas of Roman lopsided dice, following the usual configuration—already adopted in Roman times—in which the values of the opposite sides must add up to 7 (1-6; 3-4; 2-5). As the volunteers had no incentive or preconditioning to favour one number or the other, the authors of the study expected the labelling to be, on average, random. To their surprise, they found that the volunteers preferred to place the number 6 on the longer side, replicating the Roman pattern. When asked why, the answer was as logical as it was surprising: it is easier to paint the largest number of dots on the side with the largest surface area. Paradoxically, this explanation reinforces and nuances the least valued hypothesis, that of technical limitation.
Brainteaser 3: Five Roman dice
And now what would be a Roman’s solution to these dice rolls of five in five?

Solutions
Miguel Barral
Comments on this publication