What’s the best way to approach (and successfully solve) a mathematical problem statement? Perhaps by drawing a picture? That, at least, is the conclusion of a striking new study by researchers at the Universities of Geneva and Burgundy.
It’s not a trivial assumption. It is thought that when we face a mathematical problem that contains both mathematical information (numbers and arithmetic operations) and non-mathematical information (the context of the problem and the characteristics of the entities involved), our brains process this combination of verbal and numerical information and convert it into a mental representation in order to identify the best strategy for solving it. On the other hand, more and more studies suggest that the schematic drawings that are usually made to solve this type of problem are a reflection of these mental representations.
Game 1: Not a game, an experiment
In the study, participants were asked to solve 12 simple arithmetic problems in as few steps as possible and to draw a picture that would help them understand and solve the problem.
Here are two of these problems, and we invite you to solve them in the same way: in as few steps as possible, and with a drawing to help you understand the problem.
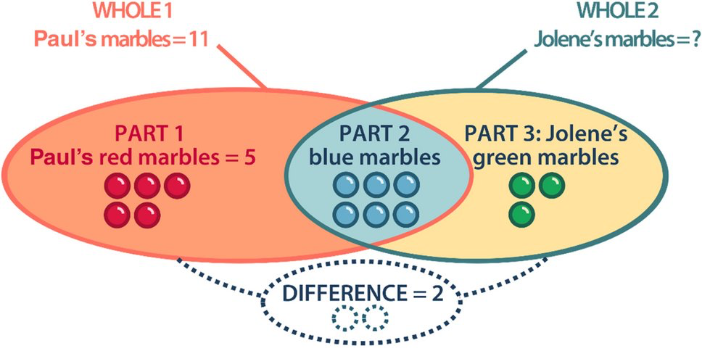
Problem 1: Paul has five red marbles and also has some blue marbles. In total he has eleven marbles. Julie’s marbles are green and blue. Julie has as many blue marbles as Paul and also has two fewer green marbles than Paul has red marbles. How many marbles does Julie have?
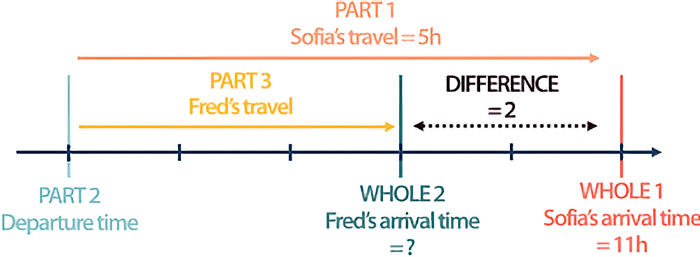
Problem 2: Lisa takes the train during the day, travels for 5 hours and arrives at her destination at 11am. Fred got on the train at the same time as Lisa and his trip took 2 hours less. What time did Fred arrive at his destination?
Independently of the above, many studies postulate that relying on drawings, diagrams or other types of graphical representations when processing information has numerous benefits: it improves our ability to learn and remember, it helps us to understand complex concepts, it reinforces critical and scientific thinking, and it fosters a transversal and interdisciplinary interpretation. And from a mathematical point of view, using these representations makes it easier to establish the relationships between different data, to visualise the information implicit in the statement and to identify the most direct and simplest solution strategy.
Game 2
Use the drawings to answer these complex and hieroglyphic questions.
A recent study goes a step further by suggesting that the verbal information in the problem statement influences the type of diagram shown and also the strategy chosen to solve the problem. More specifically, the study has found that the type of diagram preferentially chosen depends on whether the statement is cardinal or ordinal in nature.
Thus, when the context alludes to the cardinal properties of the quantities involved—the number of elements in a set—a drawing based on groupings of entities (crosses, circles, etc.) that sometimes overlap (or intersect) is usually chosen. This in turn leads to a three-step arithmetic strategy. On the other hand, when the statement of the problem focuses on the ordinal properties of numbers—the position they occupy in a set—we usually opt for drawings based on axes, graduations or intervals, which lead to a more direct and simpler one-step solution strategy.
And this is observed even when the problems are analogous from a mathematical point of view: they have the same structure, the same numerical values and can be solved with the same strategy (as in the case of the two problems in Game 1).
But perhaps the most interesting reflection is that, knowing this, it is possible to guide and train the student to apply this second type of diagram, thereby facilitating the identification of the best way to solve it.
Game 3: A high-flying challenge
Sara wants to travel from Madrid to Tokyo. To do so, she flies first to New York, from where she takes a plane to London and from there to Tokyo.
Paul also wants to go from Madrid to Tokyo, but in his case he flies directly from Madrid to London and then takes a flight to Tokyo.
If Sara flies for a total of 27hrs 15min and Paul for 14hrs 30min, and given that the flight from New York to London takes 4hrs 45min longer than the flight from Madrid to London, and the flight from London to Tokyo takes 12 hours, how long is the flight from Madrid to New York?
And if both Sara and Paul lose only one hour at each stopover, what will the local time be when they each arrive in Tokyo if they both depart Madrid at 2pm?
Solutions
Comments on this publication