Magic squares are one of the most fascinating mathematical artifices, and also one of the most reflected in art, from Dürer’s engravings to Gaudí’s Sagrada Familia. This is something inspired by the magical properties—both the purely numerical as well as the divinatory and protective ones—that have been attributed to them throughout history.
Magic squares are numerical dispositions of natural numbers (or positive integers) of n rows and n columns (or, in other words, of order n), and where the numbers that are inserted go from 1 to n2. The magic arises because the sum of the numbers present in each row, in each column and in each main diagonal, give the same result, called the “magic constant” or the “magic sum.”
It is likely that the most recognised magic square is that included by Albrecht Dürer in his engraving Melencolia. It is a square of order 4, teeming with magical properties, since the sum of any of its four quadrants also results in its magic constant: 34. And the same happens with the sum of the four central numbers. In addition, the central squares of the lower row are occupied by 15 and 14, representing the date of the engraving: 1514.
With all these clues, you should be able to complete Dürer’s magic square:

Lo Shu Square
Dürer’s magic square is probably the best known, as well as the first representation of one in Europe, but the truth is that by the time the artist represented it, magic squares had already enjoyed a long history.
The first reference dates back to China in the year 2200 BC. According to legends concerning the Emperador Yu, in ancient China there was a huge deluge. The people offered sacrifies to the god of one of the flooding rivers, the Luo river, and a turtle emerged with a strange dotted pattern on its shell, the Lo Shu square . It was a 3×3 grid where the numbers were represented by groupings of dots.

With the divinatory and protective characteristics that were granted to them going hand in hand, the magic squares would have travelled from China to the rest of Asia, and from there to Egypt, where they were included in clothes and ornaments as talismans.
It is believed that the first to deepen and study their mathematical properties were Arab scholars and the Islamic world, who made them known in Europe in the fifteenth century, where they permeated immediately owing to their supposed magical properties, first those related to divination, alchemy and astrology, and later the purely mathematical ones.
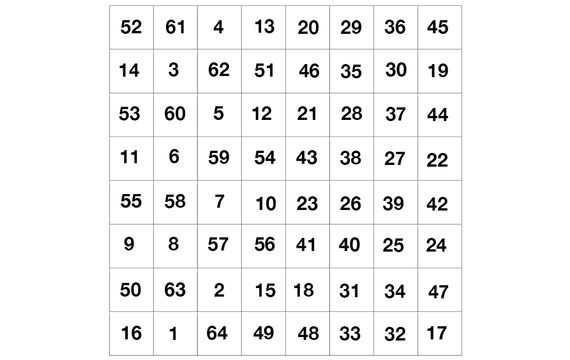
Franklin’s semi-magic square
The American polymath Benjamin Franklin was also a great creator of first-rate magic squares. In 1750 he published a semi-magic square of order 8 and with a magic constant of 260. It is said to be semi-magic because as well as its ordinary attributes, each half-row and half-column add up to 130, i.e. half the magic constant. What’s more, the sum of the four corners and the four central squares is also 260. With that information, the magic square below can be completed:

Into the facade of Sagrada Familia
An example showing that magic squares have never lost their mystical or divine essence is the fact that Antonio Gaudí incorporated into the facade of his whimsical Sagrada Familia, dedicated to the Passion of Jesus, a pseudo-magic square of order 4 with a magic constant of 33, the age of Christ. In this case it is pseudo-magic because, instead of including the first 16 numbers, there are two missing (12 and 16) and two that are repeated in consecutive boxes. Knowing this, you can try to complete it.

See the solutions to the three proposed challenges:


Comments on this publication