For this new challenge for the readers of OpenMind, we were inspired by the one that the mathematician Jacob E. Goodman proposed in the magazine American Mathematical Monthly in 1975: the so-called pancake problem. Although nobody has managed to solve it yet, the best approach for almost 30 years was written by Bill Gates in his only article of scientific research.
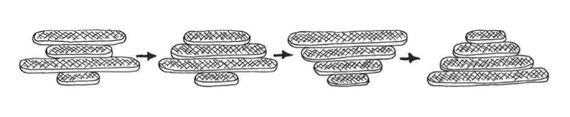
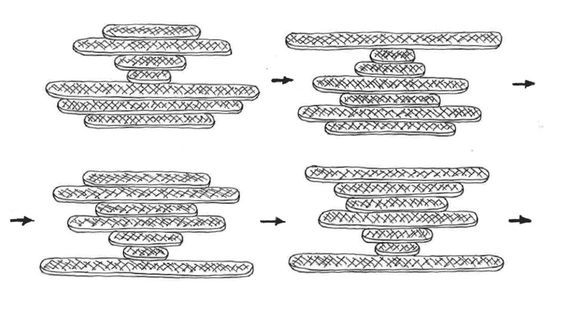
Our brainteaser, much more accessible, consists in ordering the stacked pancakes by size, starting with the largest one (bottom) and ending with the smallest one (on top). We have three games:
Game 1

Game 2

Game 3

In all three cases the objective is the same: you have to make the smallest possible number of moves with the spatula to achieve the desired arrangement.
Each move consists in inserting the spatula at a certain height of the pile, lifting it with all the pancakes that are on top and, with a quick twist of the wrist, placing them flipped over on the top of the pile.

The original problem
To help solve it we recall the original problem from 1975, in which Harry Dweighter is a harried waiter who finds himself with a pile of pancakes coming out of the kitchen. How many movements at most does he have to make to leave the pancakes perfectly ordered?
The question immediately captivated mathematicians and computer scientists. Programmers were interested because it could have applications for helping to reorder data. And it is also the kind of problem that mathematicians are passionate about: it seems very simple, but the solution becomes more complicated as the number of pancakes increases.
If we have a stack of 3 pancakes, in the worst case you will have to make 3 movements (it is easy to check in this video); if we have 7 pancakes, at most there will be 8 moves; with 11 pancakes it’s 13 (here we already need a computer to calculate the result); with 19 pancakes it’s 22 moves; and with 20 pancakes, nobody knows! It could be 23, or 24, or even 25… But given the difficulty in calculating all the permutations of pancakes and strategies for moving them, it hasn’t even been possible to demonstrate the solution with the help of today’s most powerful computers, after four decades of computing evolution. What was achieved (and relatively quickly) was a formula that established the upper limit of the necessary number of movements.
Gate’s achievement
In 1979 a study showed that the required number of changes in a stack of n pancakes is always less than (5n+5)/3. In other words, if we have 20 pancakes of different sizes and randomly arranged, in the worst case it’s sure that more than 33 movements would never be necessary to order them to the satisfaction of Harry Dweighter. The authors of this work were Christos H. Papadimitrou and William H. Gates. Yes, that’s the same Bill Gates who had already founded Microsoft. It took almost 30 years until, in 2008, Gates’ achievement was surpassed by a team of researchers from the University of Texas at Dallas, who established that upper limit at 18n/11. Hence we can assure the harried waiter that 32 movements will always be enough to order 20 pancakes.
The article by Gates and Papadimitrou incorporated an even more twisted variation of the original problem, known as the burnt pancake variant, in which pancakes are burnt on one hand, so that in addition to ordering them correctly by size they must also be placed with the burnt side face down. But we leave that wrinkle for future challenges.
Solutions:


Comments on this publication