Before becoming one of the most renowned mathematicians (and physicists) in history, Frenchman Blaise Pascal demonstrated an amazing aptitude for higher mathematics. While still a teenager, he wrote an essay that elevated him as one of the most brilliant and promising mathematicians of the time in the eyes of his colleagues. Despite his fragile health and short life – he died at the age of 39 – he left his mark on the history of physics as well as computer science.
The precociousness of Pascal (19 June 1623 – 19 August 1662) is even more surprising when one discovers that during his first years of training he had no access to the discipline of mathematics. The young Blaise was instructed at home by his father, a respected mathematician, who forbade him access to any mathematical text until he turned 15 years old. This censorship intensified the interest of young Blaise, who began to teach himself mathematics. Thus, at the age of 12, he demonstrated that the sum of the angles of a triangle is always equal to 180°. Faced with the evidence, his father finally relented and gave him a copy of Euclid’s The Elements.

At the age of 14, Pascal was already attending meetings of the “academy” of polymath Father Mersenne, which brought together distinguished mathematicians in the priest’s cell to discuss and exchange ideas. And when he was barely 16 years old, he revealed all his talent with the aforementioned Essay on Conics (1639), in which he enunciated what has come to be known as Pascal’s Theorem or the Hexagrammum Mysticum Theorem.
From games of chance to the search for faith
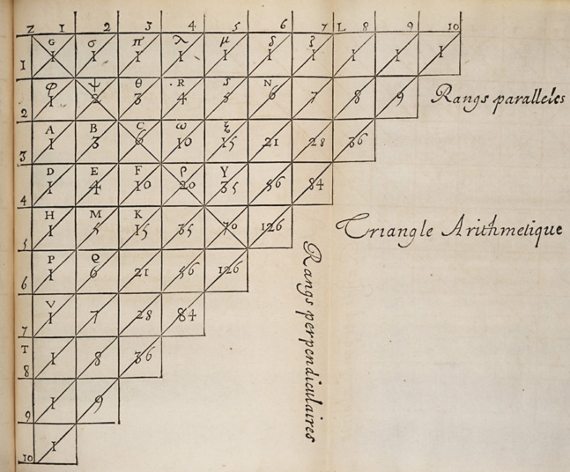
This was the early start of a professional career steeped in achievements, discoveries and contributions, which was to reach its climax in 1654 thanks to a professional Parisian gambler, Antoine Gombaud. Forced to leave a game of chance unfinished, he turned to Pascal to determine the fairest way to distribute the pot. The question aroused the mathematician’s interest and led him, in collaboration with Pierre de Fermat, to establish the fundamental laws of probability – a process in which he introduced the so-called Pascal’s Triangle.
Based on an idea that was revolutionary at the time (when a coin is flipped, it is equally likely to come out heads or tails), they founded a new branch of mathematics: the theory of probabilities, which is now applied to a multitude of questions in the most diverse fields, from climatic or epidemiological models to the prediction of stock market fluctuations.
Pascal was so enthusiastic about the possibilities offered by this new mathematics that he even became convinced that with it he could justify the need to believe in God, the essence of faith. According to Pascal, “the excitement that a professional gambler feels when he makes a bet is equivalent to the amount he can win multiplied by the probability of winning it”; and this led him to argue that since the potential prize of eternal happiness has an infinite value, then religion, the need to believe, is nothing more than a form of infinite excitement. Ironically, that same year, in 1654, and shortly after experiencing what he described as a profound mystical experience of conversion, Pascal decided to consecrate his life to Christianity and confined himself to the convent of Port-Royal.
But before that, Pascal’s name had resonated throughout the continent thanks to a prodigious invention, the Pascalina, the fruit of years of dedication. In 1642, Blaise Pascal had begun work on an instrument that would facilitate his father’s work as commissioner of finance in Rouen, a position that obliged him to spend much of his time making tedious calculations involving enormous sums of money for which he could only be helped by the abacus. Only a few months later, young Blaise (who assisted his father in this task) built the first mechanical calculating machine – or one of the first and, without doubt, the most sophisticated.
Father of the Pascalina, godfather of PASCAL
During the following years he would continue working on the device in his eagerness to perfect it, completing up to 50 different models; in 1649 he obtained a “privilege” (the equivalent of a patent at the time) on the machine. Finally, in 1652, he gave the first public demonstration of his invention in Paris, whose fame spread throughout France and the rest of Europe. In essence, the Pascalina consisted of a box, the interior of which housed a complex set of gears, wheels and cylinders that were driven through a collection of rotors located on one of the sides. When they were turned, the calculation mechanism was activated and the result appeared in the form of digits in some displays or windows located in the upper part of the box.

Because of this invention, Blaise Pascal is considered the father of calculation machines, precursors of the first computers; and that is why, in 1970, the Swiss electronic engineer Niklaus Wirth named the programming language he had just created PASCAL, which was the gateway to computing for many students at the end of the 20th century. But his scientific legacy actually has much more to do with physics than with computers; Pascal (Pa) is also the name of the unit of pressure of the International System (1 atmosphere = 101,325 Pascals) in recognition of that momentous work, which led him to investigate how atmospheric pressure varies or to enunciate Pascal’s Principle and apply it to inventing the syringe and the hydraulic press.
Comments on this publication