Exactly 100 years ago, in 1918, the German physicist Max Planck was awarded the Nobel Prize for Physics “in recognition of the services he rendered to the advancement of Physics by his discovery of energy quanta.” The quantisation of energy means that the particles, when vibrating, do not emit radiation continuously, but instead release it as discrete packages with a specific energy content.
It is a difficult idea to understand, which Albert Einstein liked to explain by using the analogy of a keg of beer whose contents could only be dispensed in quarter-litre bottles. In other words, the beer tap of that imaginary and quantum keg could only serve that specific quantity in each pull, that is to say, a quantum of beer.
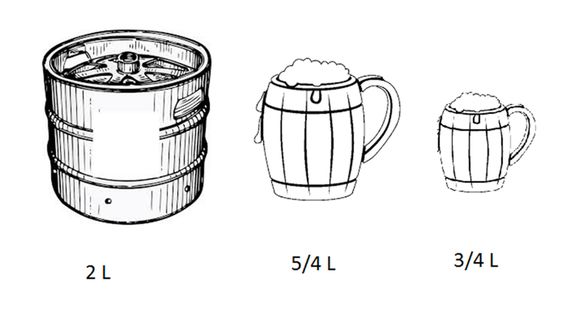
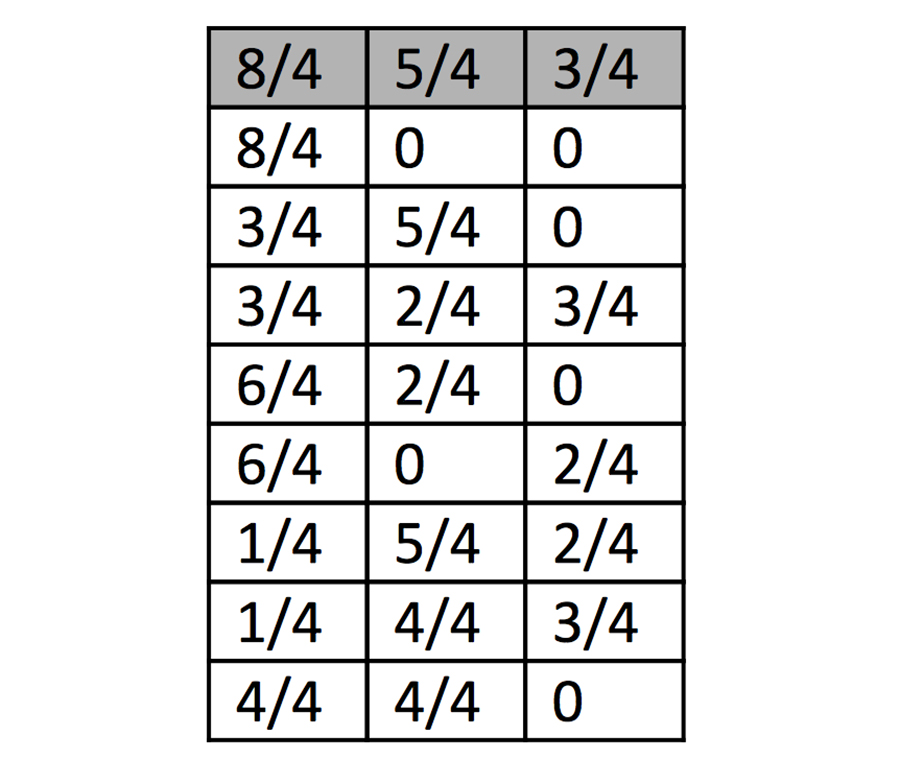
Here we present a brainteaser that extends this analogy. Let’s suppose that Einstein has a 2-litre beer keg and wants to divide it equitably with Planck, an operation for which he has two empty containers, one with a capacity for five quarters of a litre and another with a capacity for three quarters of a litre. Which steps should Einstein follow do to divide his quantum beer keg into two equal parts? (Assume that you can return beer to the keg.)
The history of quantum
The history of quantum began in 1900, the year in which Max Planck was working on the problem of radiation emitted by a black body and its dependence on temperature. After amassing a huge amount of experimental data, he managed to deduce a mathematical formula that fit those values. But at the same time, that formula posed a dilemma: it only worked if it was assumed that, when they vibrated in their positions, the constituent particles of the body did not radiate energy continuously, but did so in a discrete or “quantised” way. It was as if the particles emitted individual energy packets whose energy content depended on their frequency—to go more deeply, the value of that quantum was the product of the frequency multiplied by a fixed value, which we now know as the Planck constant.
In the eyes of Planck, a physicist from the old school, that result was “nonsense.” He consoled himself by thinking that he had found a mathematical trick that fitted the experiments quite well; meanwhile he was convinced that another colleague would soon come along who would be able to provide a better explanation for the phenomenon.
What Planck could not even imagine at that time was that some physicist would take his formula so seriously that he would propose that those quanta could be real entities. That physicist turned out to be the young and, at the time, unknown Albert Einstein.

Not only that, but he also had no qualms about stating that the quantisation of energy implied that radiation was a stream of discrete particles, and not a continuous electromagnetic wave, as it was considered by classical physics. That interpretation broke all the moulds, but Einstein assumed it naturally, as a logical consequence of Planck’s formula.
Returning to the analogy of the beer keg, from the point of view of classical physics and Planck, the keg would be filled with a single volume of beer and quantisation would be a consequence, a limitation, of the mechanism of the dispensing device. However, what Einstein was proposing was that if the keg were opened, we would not find one volume of liquid, but a set of small volumes or quarter-litre packs of beer. The quantisation would not be a consequence of the tap, but of the very nature of the beer in the analogy. And of light in reality.
That hypothesis, incredibly radical and revolutionary at the time, allowed Einstein to explain the “photoelectric effect”—which, like the problem of the radiation of a body, could not be explained by classical physics—in his now celebrated first paper of 1905. Despite this, Einstein ideas would still take years to become generally accepted. In fact, just a few years later, when Einstein aspired to occupy some academic position, the same Planck wrote a letter of recommendation for him in which urged the recipient not to take into account Einstein’s ravings about energy quanta when assessing the young man’s capabilities.
A quantum of beer for Einstein and Planck
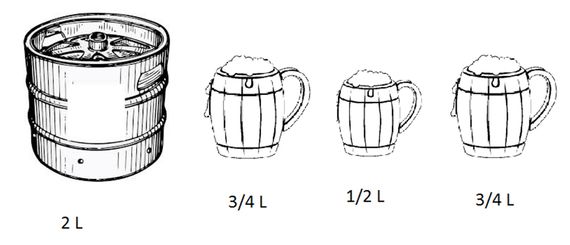
Now let’s go back to our problematic 2L beer keg. The second challenge is to provide Einstein and Planck each with exactly one quantum (= one quarter litre) of beer for them to toast each other. For this you have three mugs, two with the capacity for three quarters of a litre each and one mug that holds half a litre. The goal is to serve two mugs of beer each with a quarter litre. Again, assume you can return beer to the keg.
Solutions
 Solution for the second problem:
Solution for the second problem: 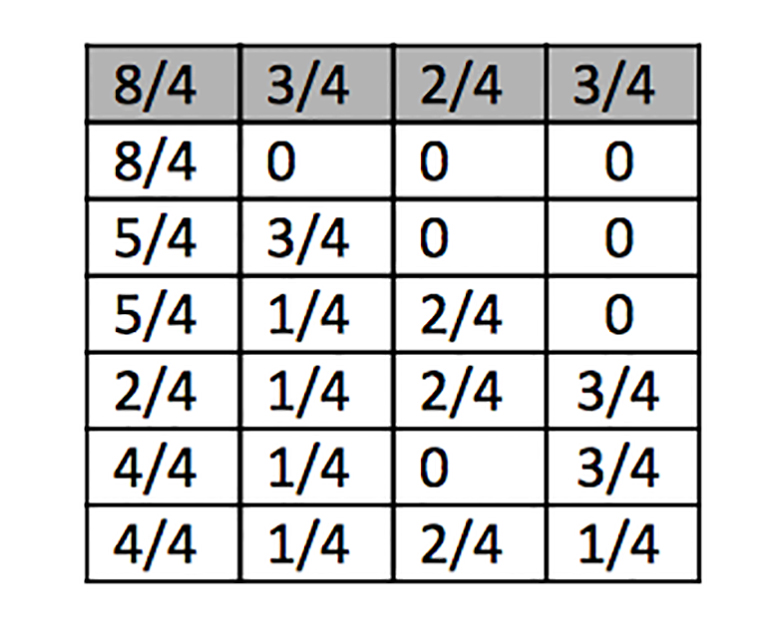
Comments on this publication