What does Santa Claus have to do with a group of Danish mathematicians? The answer is the classic mathematical problem of the single-source shortest path, which has been a headache for mathematicians for over half a century. But it is also the kind of calculation that underlies the apps we rely on for our daily travels. The discovery of an algorithm that provides the solution in an instant will be much appreciated by Santa, as it will make his traditional but laborious Christmas Eve deliveries that much easier.
The so-called shortest path problems encompass those graph problems with several vertices (or nodes) interconnected by segments with an assigned value, and where the challenge is to find the shortest path between one of the nodes and one or more of the other nodes.
Brainteaser 1: The classic shortest path mathematical problem
This category of mathematical problem includes the so-called single-source shortest path problem, which deals with the specific case of finding the most favourable path between the starting node and all the other nodes that make up the network or network.
In our brainteasers, the most favourable path is the one that gives the lowest final score (summing the score of each leg); note that this path is not necessarily the one that consists of the fewest legs or steps. We can see this in the example below:
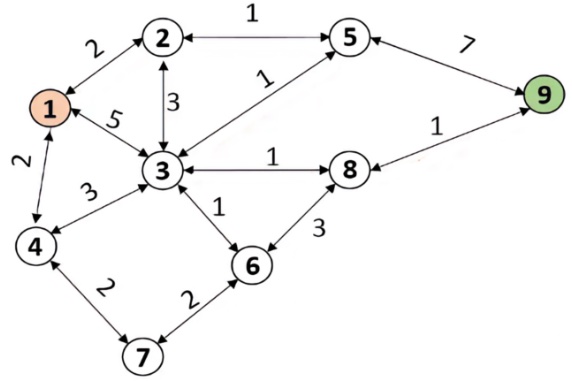
Solution: The most favourable route from node 1 to 9 is the one that makes the route 1-2-5-3-8-9 (2+1+1+1+1= 6).
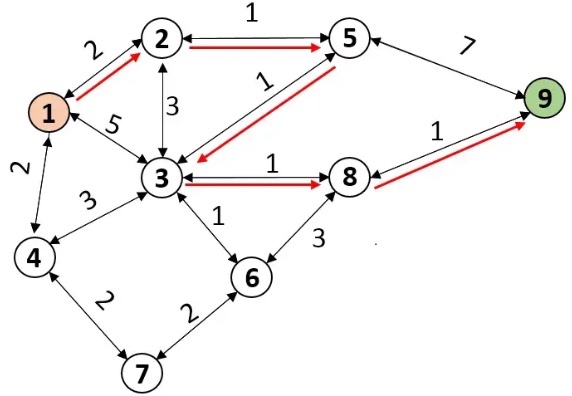
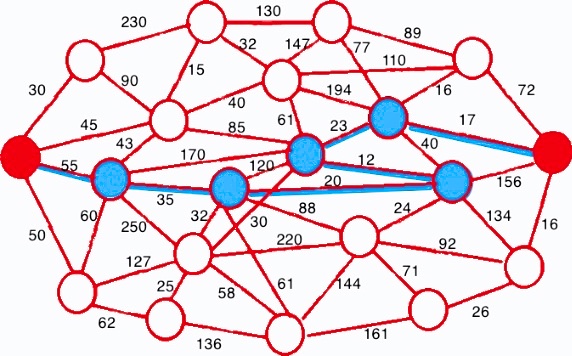
Following the reference of the previous example, determine the best route to go from one of the red nodes to the other:
Formulated—at least formally—in the 1950s, since then the problem of finding a definitive algorithm to solve it immediately has challenged mathematicians all over the world.
How has this problem, at first glance not that complicated, withstood the assault of some of the most brilliant minds for so long? The key lies in the concept of the most favourable route, which is not necessarily the shortest, a difference that derives from something called negative weight, a way of weighting and quantifying factors that favour (or penalise) one route over another. This is easy to understand if we consider that it takes less energy to cover 1 km over flat terrain than to climb 500 metres up a steep slope.
The key behind the optimal route
This is precisely the type of problem and calculation on which the apps we use in our daily lives—such as Google Maps—are based to guide us along the optimal route depending on distance, financial cost or time.
Taking into account the negative weight complicates the solving of the problem. Until now, algorithms were used that required a large amount of computation, which delayed the solution. But that is about to change, as a team of mathematicians and computer scientists at the University of Copenhagen has discovered an algorithm that solves the problem in an instant. The key has been to introduce an extra dimension into the calculation to reflect the negative weight, thereby turning the two-dimensional graph into a three-dimensional network.
This solution comes just in time for its application, for example, in the booming electric vehicle industry. For such cars, which recharge when travelling downhill, the slope is the key factor in determining the best route. But it will also be very useful in other areas, such as the stock market or currency trading. And it’s a welcome tool when you’re driving a sleigh laden with presents and have to climb up an enormous number of chimneys with a large sack on your back.
Brainteaser 2: Santa Claus and the single-source shortest path problem
Help Santa Claus solve his single-source shortest path problem. In other words, find the shortest paths for Santa to get to each chimney starting from the chimney where his red hat is already sticking out. And as an additional challenge, also find the shortest path from the initial chimney to E, passing first through A.
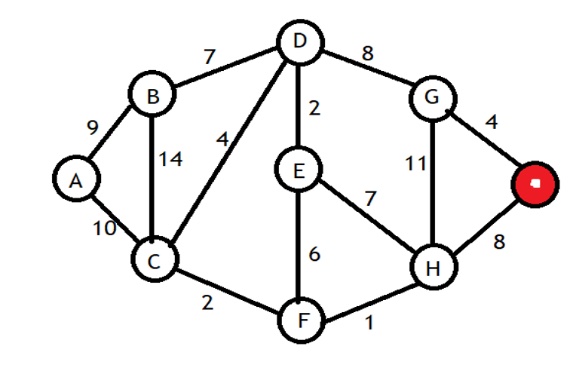
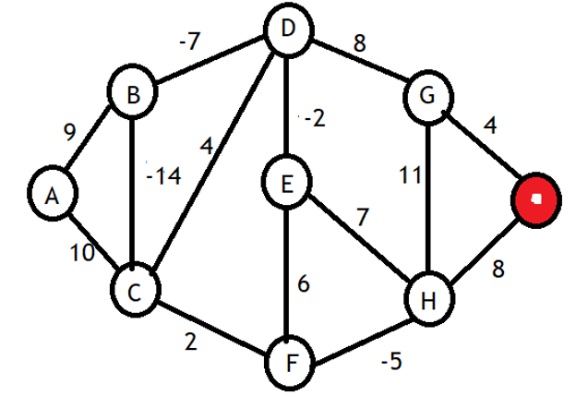
Brainteaser 3: Santa Claus doesn’t always see the downside of climbing up chimneys
It might look the same as brainteaser 2, but it’s not the same, as it now includes negative weight. Otherwise the rules are the same: find the best single-source paths from the chimney from which Santa emerges, to each of the other chimneys. And don’t forget the extra challenge: discover the most favourable path from the initial chimney to E, passing first through A.
Solutions
Comments on this publication