Newton’s mathematical revolution conceived on his farm while he was in seclusion from the bubonic plague meant that the figure of the mathematician came to be considered as essential in European societies and courts in the 18th century. Experts in the field evolved from being mere aficionados of numbers to becoming respected professionals capable of solving a wide range of practical problems, from architectural and social to ballistic and naval.
The great powers vied for the services of the best mathematicians, often reserving for them the role of advisors to their top leaders. And, without a doubt, the most respected and important mathematician of the time—and one of the most important in history—was the Swiss genius Leonhard Euler, who spent most of his professional career at the courts of Prussia and Russia, in the service of Frederick the Great and Catherine the Great, respectively.
Among the most important practical problems solved by Euler were the prediction of the phases of the moon at distant dates, basic information for the preparation of tables for ocean navigation, and the development of the algorithmic method, a fundamental tool for mathematicians even since then, and one that is still used today in fields such as physics, chemistry and economics.
However, the most famous problem in which Euler was involved and which helped to raise his profile was the one known as the Königsberg Bridge Problem, in reference to the ancient Prussian city that later became the Russian city of Kaliningrad. This problem was the starting point for Euler to develop some of his most important theorems.
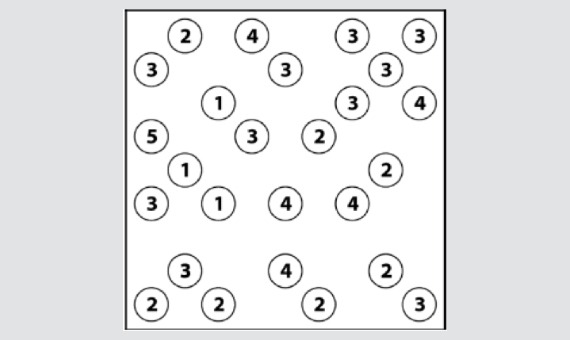
Game 1
Connect all the islands in the diagram together using the following rules:
- The number inside each island indicates how many bridges are connected to it.
- Each pair of islands can only be connected to each other by a maximum of two bridges.
- Bridges can only connect islands in straight non-diagonal lines; they have to begin and end on an island and cannot cross each other.
Example:


Built on the sandy banks of the Pregolya River, Königsberg consisted of four separate neighbourhoods connected by seven bridges, which attracted numerous visitors. Many people wondered if it was possible to follow a route that would allow them to cross all the bridges without crossing any of them twice, something that seemed impossible and, in fact, was impossible. Euler set out to prove this mathematically, and in his endeavour he invented a new form of mathematical representation: graphs. In formulating Euler’s Theorem, he also laid the foundations of graph theory, the branch of mathematics that deals with the study of graphs.
Euler took the map of the city and developed a minimalist representation in which each neighbourhood was represented by a point (also called a node or a vertex) and each bridge by a line (also called an edge). In other words, he represented it with a graph.
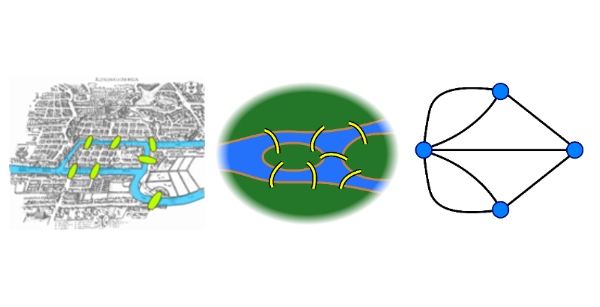
From this first graph, he deduced that in order to plot the desired route, and if the starting point is the same as the ending point—that is, the route begins and ends in the same neighbourhood, forming a closed circuit—each point should be linked to an even number of lines, since each time the traveller crosses a land mass he must enter by one bridge and leave by a different one. If, on the other hand, the journey begins and ends in different places, then the starting and ending neighbourhoods can have an odd number of bridges. Since in Königsberg the four land masses were connected by an odd number of bridges, it was impossible to draw the desired route.
But more importantly, Euler generalised from the Königsberg graph that it is possible to traverse any network without passing through the same line twice if all points are connected to an even number of lines or if two points are connected to an odd number of lines.
Today, graph theory is applied to solve practical problems in many disciplines and fields: game theory, artificial intelligence, resource optimisation, classification and even maze design and solving.
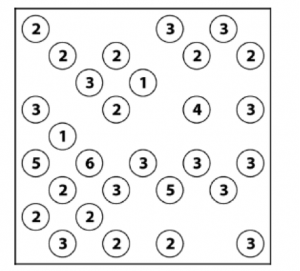
Game 2
In addition, by reducing the problem to a graph, dispensing with aspects irrelevant to solving the problem such as the length or curvature of bridges and the dimensions and contours of neighbourhoods, Euler also laid the foundations of topology: the mathematical branch that studies only the essence of objects, as opposed to geometry, which studies the exact shape and size. The great advantage of topology is that it makes it possible to represent in a very visible way the relationships between different entities and thus to visualise more easily the best way to reach the desired result or solution.
One of the most popular and well-known applications of topology is the representation of the routes of the different public transport lines—subway, bus or railway—in which the stations and tracks that connect them are represented as points and lines, allowing the user to identify at a glance which is the shortest way to reach their destination and at which stations they should change lines.
Game 3
Solutions
Miguel Barral

Comments on this publication