They are known as einsteins, not in reference to the famous physicist, but as a word play on the German expression ein stein, meaning one stone. Although in this case it would be more appropriate to translate it as one tile, referring to a closed shape that can cover a surface without leaving any gaps. In short, a tessera, but with unique characteristics that have led to the solution of one of the great mathematical mysteries.
Einstein-type tesserae or tiles are characterised by the fact that they are aperiodic, which means that when arranged together as a mosaic, they are capable of covering an infinite plane in its entirety, but at the same time, without forming repetitive patterns, so that no kind of symmetry can be discerned. However one divides up the mosaic, each section is unique, none repeating the pattern of another. Einsteins are the mosaic equivalent of irrational numbers.
This design seems incredible or impossible because it is hard to imagine that in an infinite extension no two regions or sections, however small, could coexist with the same tessellation layout. In fact, for more than half a century, mathematicians have doubted that it was possible. And then, in March 2023, the discovery of “the hat” was confirmed: the elusive einstein.
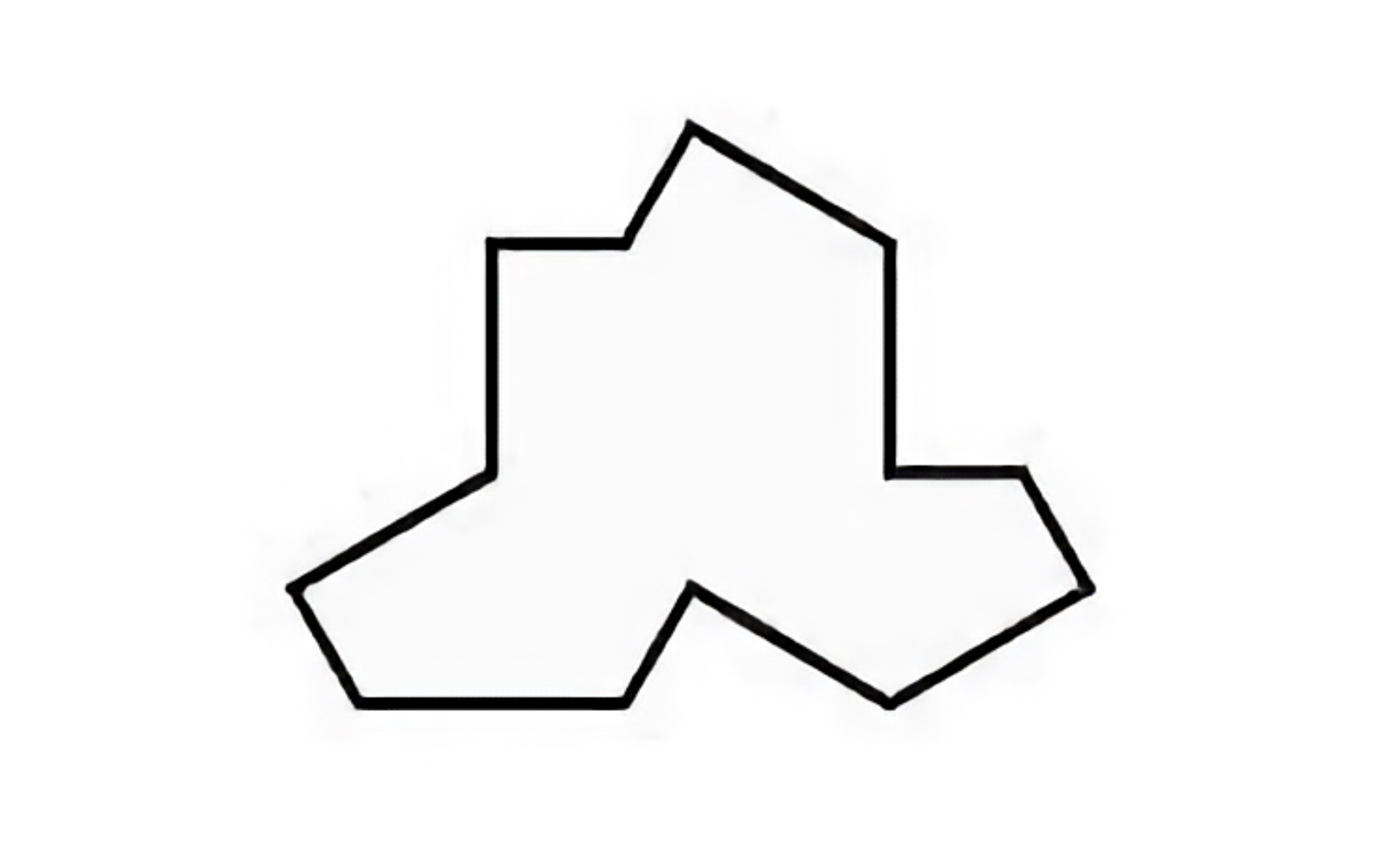
Game 1: Has anyone seen my hat? And my turtle?
Almost as soon as it was presented to the public, the hat was adopted by various artists and creators as a motif for their designs, some of which are real games in themselves. For example, in this composition created by the American artist and mathematician Robert Fathauer, you have to identify how many shirts and how many hats there are:
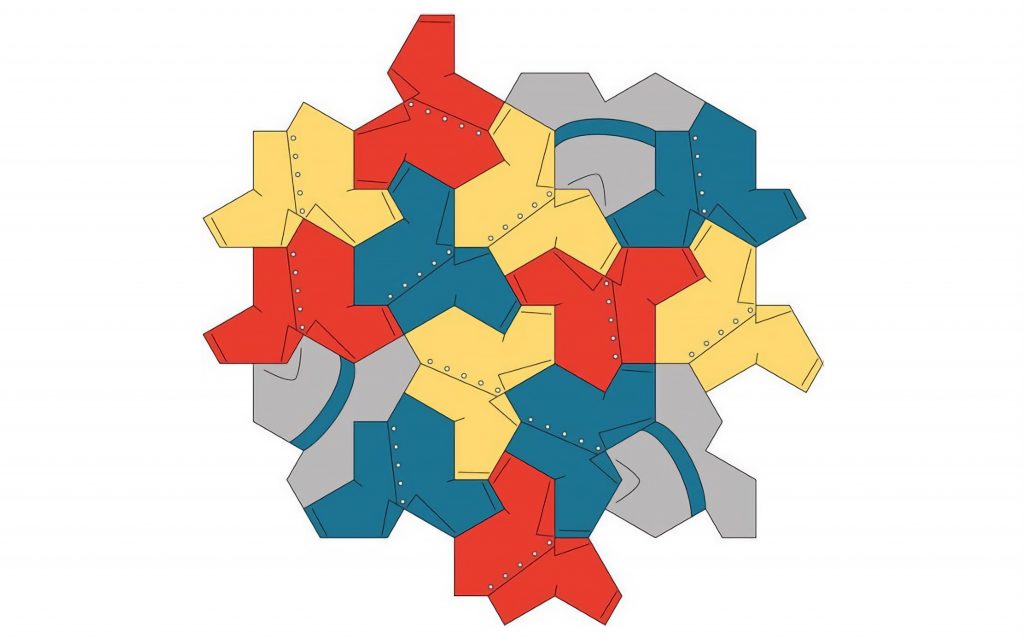
Credit: Robert Fathauer
In this mosaic, the hats have been transformed into turtles and the challenge is to identify the other reflected turtle, the one whose head is turned to the left:
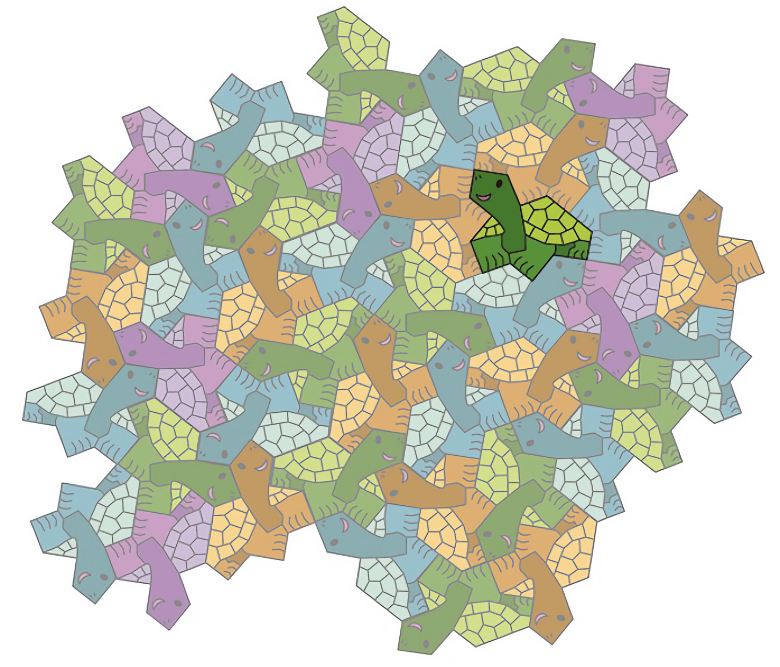
Credit: Yoshiaki Araki
The problem of the existence or non-existence of this type of shape began in 1961, when the Chinese mathematician Hao Wang formulated the so-called “Wang’s conjecture“, in which he suggested that any set of shapes or tessellations that can cover a space in its entirety also allows for a periodic tessellation. This conjecture, however, was disproved just five years later, in 1966, by the mathematician Robert Berger, who also identified the first set of aperiodic pieces: a “monster” of 20,426 tile shapes able to prove aperiodicity.

From that moment on, many mathematicians set out to discover an ever smaller set of shapes. This quest was spearheaded in 1974 by the brilliant physicist and mathematician Roger Penrose, who presented an elegant solution based on two very simple shapes christened “the kite” and “the dart”.
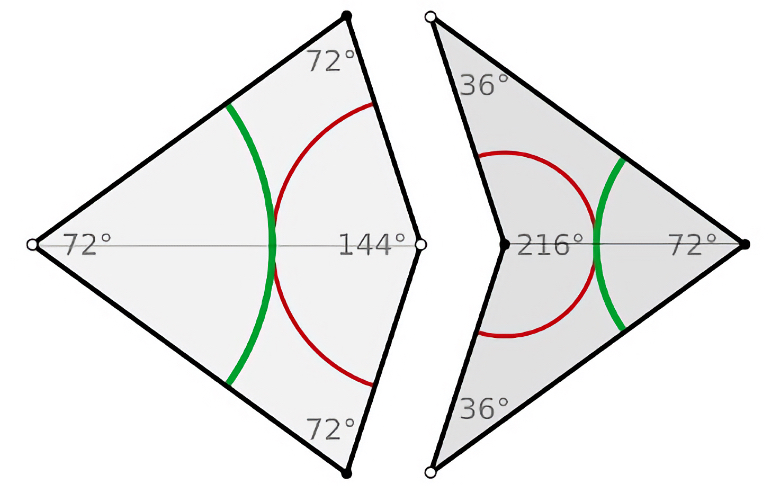
The physicist and mathematician Roger Penrose presented an elegant solution based on two very simple shapes christened “the kite” and “the dart”. Credit: Own design
Since then, and despite ongoing effort, no one had managed to reduce the number of shapes to a minimum. That is, to find a single design capable of tessellating an infinite surface without any periodicity.
Game 2: Do you like puzzles?
In this game, the aim is to fill in each of the boards by fitting the accompanying pieces together:


In a twist of fate, a few months ago, in November 2022, David Smith, a retired British maths enthusiast, managed to solve the elusive puzzle. First, by playing with a computer program that allowed him to design and assemble different shapes. Then, when he found a promising design, he cut out a number of pieces on paper to experiment with. It was in this way, almost as if playing a children’s game, that he discovered “the hat”, an astonishingly simple 13-sided polygon that nevertheless fulfils the requirements to be an einstein. Or rather, to be the first einstein. This property has just been demonstrated by the computer scientist Craig Kaplan—to whom Smith turned to when he became aware of his discovery—in collaboration with other mathematicians, in a paper that has revolutionised the mathematical community. All the more so because the design discovered is not unique, but only the first of a whole continuum of einsteins that are obtained by modifying the ratio and size of the sides of the original hat shape.
Game 3: The ultimate challenge: cut-and-paste
Like a child’s game, the challenge is to tessellate this space with the hat. You have to arrange 22 hats (the first one is already in place) in such a way that they completely cover the surface without going outside the margins. It is advisable to use the method applied by David Smith: cut out a set of paper pieces and try to fit them together.
Solutions



Comments on this publication