The year 2018 marks the thirtieth anniversary of the publication of Foucault’s Pendulum, the second novel by Umberto Eco, which was a literary phenomenon. In the story, the Italian semiotician puts the reader on the trail of a supposed cosmic plan—drawn up in the time of the Knights Templar—which develops secretly from then until the setting for the novel’s action at the end of the 20th century. Its three protagonists are caught up in the search for the “fixed point” on the Earth’s surface where the culmination of the plan will take place, and whose unknown location would be marked by a Foucault pendulum.
But just because the location is secret doesn’t mean that it can’t be found:
- In fact, its latitude can be determined by virtue of the time a Foucault pendulum takes to complete one full circle at that point, as the protagonist trio of the novel well knew:
«At certain places on the globe the Pendulum completes its circle in thirty-six hours; at the North Pole it takes twenty-four hours; at the Equator the cycle doesn’t vary with the season. So the location matters,» says one of them.
- Regarding the longitude, it is enough to know the time at the location and compare it with the time on a clock that keeps the time of a reference place (whose longitude is known): e.g. the time on the Greenwich meridian.
Here we challenge you to calculate the location of this other Foucault pendulum, which in exactly 5 hours covers an arc of 60.15 degrees (clockwise):
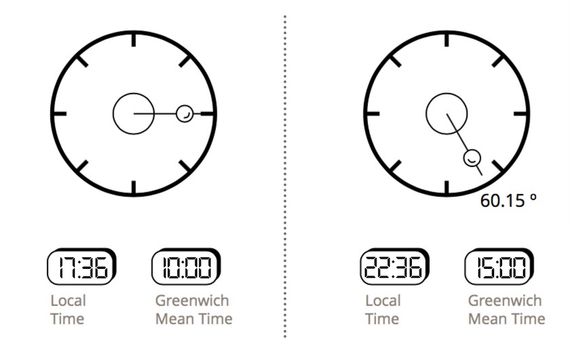
This should be a solvable challenge if we take note of the two previous clues. And in our search for the mathematical keys to this brainteaser, the history of the original Foucault pendulum can help us:
In January 1851, and with the aim of demonstrating that the Earth rotates on its axis, the amateur physicist Jean Bernard Leon Foucault (18 September 1819 – 11 February 1868) built the first pendulum of this type in the basement of his house. It consisted of a 5-kilogram weight suspended from the end of a 1.98-metre cable attached to the roof. To make the pendulum begin to oscillate without any more momentum than its own inertia, Foucault tied the weight to the wall with a rope and proceeded to burn it with a candle. After half an hour, the displacement of the oscillation plane of the pendulum became evident.
Just a few days later, the most prestigious French scientists gathered in the hall of the Paris Observatory to witness for the first time the movement of Foucault’s pendulum. For the demonstration, he held the same 5-kilogram sphere with an 11-metre cable suspended from the roof of the building. The staging was a great success. Shortly after, he held a new public demonstration at the Pantheon in Paris. The new pendulum consisted of a 28-kilogram sphere suspended from the imposing vault by a 67-metre cable. Once free, its plane of oscillation began to rotate at a speed of about 11 degrees per hour. After 8 hours it was at right angles to the original direction. And it took approximately 32 hours to complete the circumference. Since a freely suspended pendulum does not change the direction of its oscillation (once it starts), that obvious rotation could only be due to the planet’s own rotational movement.
In addition to making the first demonstration of his pendulum in the Parisian Observatory, Foucault also presented his report to the French Academy of Sciences, on 3 February 1851. In it he enunciated what is now known as “Foucault’s sine law,” a very simple equation that relates the latitude of the place where the pendulum is located with the time it takes to complete one full circle. Foucault formulated his law without any mathematical proof—beyond the observations made in his experiments at home.
As for the longitude, that very problem—determining the longitude of a place, which kept the great European naval powers in suspense during the seventeenth and eighteenth centuries—is the theme of the third novel by Umberto Eco, The Island of the Day Before. In it, one of his characters gives the last key to solving our brainteaser, in a passage that starts like this:
“I will not give you a list of the proposed methods, sir, from the one based on lunar eclipses to the one considering the variations of the magnetic needle, on which our Le Tellier laboured even recently, not to mention the loch method, which our Champlain guaranteed with many promises…”
Comments on this publication