According to Wikipedia, where I get most of my facts these days, globalization is defined as the process by which local, regional, or national phenomena become integrated on a global scale.
One common example is economic globalization: the integration of national economies into the international economy through trade, foreign direct investment, capital flows, migration, and the spread of technology.
Defined broadly, the globalization of commerce is not new: people have been trading across national and regional borders for millennia, from Phoenicians to Polynesians, from the legal Silk Route to the illegal Opium Route. However the term globalization currently refers to the explosive growth in this activity brought about by rapid advances in technology, transportation, and communication.
I want to focus here on the globalization of science, and I will limit myself to my own specialty, physics, and to my own experiences, providing a unique perspective from someone in the trenches, someone who practices science for a living. In the process of illustrating my points, I will get into some physics. I do hope you will not skip over these ideas: I have made a special effort to render them accessible to a wide audience and they are essential to fully appreciating what follows.
The motivation for trading goods is easily understood. We trade with other countries because they have what we need and vice versa: you want my cotton to spin into cloth in your mills and some-one else will turn that cloth into shirts and possibly sell it right back to me. What is being traded in the world of physics? How has the give and take evolved over the years, especially in the last two decades? That is my topic.
To set the stage I would like to discuss how physicists go about their business.
This community roughly falls into two categories: the experimentalists and the theorists.
The experimentalists build and set up measuring devices and collect data on physical phenomena: they could be looking at things that happen naturally, such as exploding stars and orbiting planets, or things they engineer in the lab, such as a piece of wire cooled to ultralow temperatures to study its resistance or particles produced in accelerators that convert the energy of the projectiles to matter. They summarize their results in the form of regularities and surprises that need an explanation.
Theorists, on the other hand, tend to stay away from fragile equipment and confine themselves to explaining the observed phenomena in terms of known laws or by inventing new ones (1). The sharp division between theorists and experimentalists is recent and driven by the extreme complexity of today’s measuring devices. In the past we had examples like Newton (1643–1727) who conducted experiments with light and Galileo (1654–1642) who studied mechanical systems and explored planets and their moons with his telescope. More recently we could also point to someone like Enrico Fermi (1901–1954, 1938 Nobel Prize) who could effortlessly switch between theory and experiment, but we would have to concede that he represents an exception.Let me illustrate this interplay between theorists and experimentalists using two of the finest players: Johannes Kepler (1571–1630) the experimentalist, and Isaac Newton the theorist. Not all examples are this glorious, but I use it because the physics involved is easily visualized.

Kepler, who accepted the heliocentric theory of Nicolas Copernicus (1473–1543), studied the motion of planets in order to answer a variety of detailed questions. What is the shape of their orbits around the Sun? What is the relation between the size of the orbit and the time (T) it takes to go around once? After forty years of painstaking data collection he summarized his findings in the following three laws around 1605.
Law 1: The planets move around the Sun in elliptical orbits with the Sun at one of the focal points.
Let me recall the definition of an ellipse. Just as the circle is a locus of a point that moves such that its distance from a fixed point (the center) is a fixed number (the radius), an ellipse is the locus of point P, which moves that such that SP+S’P, the sum of its distances from two fixed focal points (S and S’) is constant. Thus to draw an ellipse we drive two thumb tacks at S and S’, tie two ends of a string to S and S’, place a pencil at a point like P and move it around, keeping the string taut. If S and S’ coincide we get a circle of radius SP. The size of the ellipse is given by R, the semi-major axis, which is half the distance CA. When the ellipse becomes a circle, R becomes its radius.
Figure 2: Elliptical orbit of a planet around the Sun (looking down on the solar system). The Sun is at one focal point S (solid dot) there is nothing at the other focal point S’ (empty dot). If the Sun S did not exist, the planet at A moving straight up the page, would end up at B’ in a week. Instead the Sun pulls it to B.

Law 2. Area Law: The planet sweeps out equal areas in equal time.
The notion of the area swept is as follows. Consider A and B in the figure, which correspond to two locations of the planet a fixed time apart in its orbit, say one week, and C and D are also points a week apart but at a different time, chosen to be six months later in the figure. (The travel time of one week and the period between comparisons of six months are chosen for illustrative purposes only and can be arbitrary.) The Law says that the area SAB (bounded by the line SA, the arc AB and line BS) swept out in the first week equals the area SCD swept out in the second one week.
Law 3. The ratio T2/R3 involving the time period and the orbit size is the same for all planets.
For example, for the Earth the orbital time T is 3.156 x 107 seconds (one year) and R is 1.496 x 1011 meters (93 million miles) and the ratio T2/R3 is 2.977 x 10-19. For Mars T is 5.931 x 107 seconds and R is 2.278 x 1011 meters and the ratio T2/R3 is 2.975 x 10-19. The other planets obey the law to high accuracy as well.
Now we turn to Newton’s explanation of the regularities found by Kepler. For this he invoked two of his own inventions, the Laws of Motion and the Law of Universal Gravity.
Suppose we know that a planet is at A moving due north with a velocity shown by the arrow at A. We need to know what happens in the future. This is a typical problem in mechanics. Newton gives a complete answer to the question, but invokes many ingredients. First suppose there is no Sun. What will the planet be doing a week later? You might think the planet will move along the initial direction of motion for some distance and stop, as do all things on Earth when we do not actively push them. This slowing and stopping is due to friction. The planet on the other hand has no forces acting on (remember there is no Sun yet) and will move forever in the same direction and with the same speed (i.e., same velocity). This is Newton’s First law, the Law of Inertia. It was known to Galileo as well, but Newton went a step further and asked: what does it take to change the velocity of a body, that is, to accelerate it? The answer was, a force. He quantified the relation between the force F (the cause) and the acceleration a (the effect) through the Second Law of Motion:
F = ma (1)
This law tells us that if a body is to have an acceleration a, it must be subject to a force F, equal to the product of its mass m and acceleration. This equation does not tell us what agency is going to provide this force: for example it could be electrical or gravitational in origin; it could be someone pushing on the body. It does not tell you what force acts on a body at a given time. Finding what forces act on a body in a given situation is the second part of applying Newton’s Law. It is an ongoing process as new forces are discovered often. For example we know that two protons experience another force besides gravitational and electrical, the strong or nuclear force. But in any case, if somehow you know the force acting on a body, this equation allows you to find its acceleration.
Let us go back to the planet.
Since the planet is accelerating, there must be a force on it. Where is this force coming from? After all no agency seems to be in contact with it to exert a force. So here Newton daringly postulated a force that acts across the void of space, “an action at a distance”: his Law of Universal Gravitation says any two bodies, of mass M and m, located r meters from each other exert an attractive force
F = GMm/r2 (2)
on each other, where G is the Gravitational constant, the same for all occasions.
This is the force the Sun exerts on the planet to the left (or west in the figure). But it is also the force the Earth exerts on the Sun (to the east). However the effect of this same force is quite different on the Sun and the Earth due to their very different masses M and m. To an excellent approximation the Sun hardly moves, while the planet orbits around the Sun assumed fixed. (This is why we say the apple falls to the Earth, when in fact they fall towards each other. The forces on the two are equal and opposite but the acceleration of the Earth is F/M while for the apple it is F/m where F is the same. So the apple does most of the moving.)
Combining Equations (1) and (2) we get (G Mm/r2) = ma (3)
If in Equation (3) we now set M equal to the mass of the Sun, m that of the planet, and r the distance SA in the figure, we get the acceleration a when the planet is at A. (We could do this at any other time as well.)
How do we use this equation to figure out what the planet does next? The answer needs calculus. But here is a modest beginning even if we do not know calculus. Given the initial position and velocity at A we can estimate its position and velocity a week later as follows:
- From the definition of velocity as the rate of change of position with time, it follows that the change in its position in one week is the velocity at A times one week (expressed in seconds if the velocity was given in meters per second).
- Using the fact that and acceleration is the rate of change of velocity with time, we multiply by one week the acceleration (due to the gravitational force of known magnitude and direction at A) to predict its new velocity after one week. The new velocity will have a small tilt to the northwest due to the acceleration.
- Starting with the new position and velocity after one week, we repeat this to get the same at the end of two weeks and so on. We keep doing this every week and connect the 52 dots.
You can already see a problem with this recipe: it predicts that a week later the particle will end up vertically above A, near B’, because the initial velocity at A was vertical. (Its velocity will be slightly to the west of north due to the acceleration.) But it is supposed to be at B not B’ and moving along the tangent to the ellipse. The problem is with our naïve assumption that the initial velocity and acceleration remain the same for a whole week. We would do better if we recomputed the position and velocity every minute and still better, every second, and so on. Ideally the update must be done continually to yield the correct answer.
This is a exactly what is done for us by calculus, another subject that Newton invented (concurrently with and independently of Gottfried Wilhelm Leibnitz.) In this language
ma = (G Mm/r2 ) (3)
assumes the form
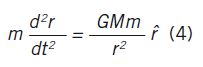
The object on the left is the second derivative of the position r (the rate of change of the rate of change computed continuously) and rˆ is the unit vector along the position of the particle. I do not expect people unfamiliar with calculus to follow this last step. It is not essential that you do, you just need to know that from now on it is a problem in pure mathematics. You can pass the buck to the mathematics department, unless you are Newton, in which case you invent the requisite math and solve the equations.
His solution (difficult even after 350 years of calculus) was a complete triumph. It reproduced all the results that Kepler had observed: the orbit was a closed ellipse, equal areas were swept in equal amounts of time and T2/ R3 came out to be the same for all planets. Not only could Newton show that T2/ R3 was the same number for all planets, he could tell you what that same number was in terms of other known quantities like G and M, the mass of the Sun. He found
T2/R3 = (4 ?2/GM). (5)
Even if you cannot follow all the intermediate details, you can at least see one aspect of the result: in Equation (3) or (4) the mass of the planet m cancels out on both sides. Since the only reference to the planet is through m, subsequent orbital properties that follow from solving the equation do not depend on the planet, as we see in the right hand side of Equation (5).
Should we be troubled by the fact that to prove the three laws of Kepler, Newton invoked two laws of his own, F=ma and F = GMm/r2 ? After all, when you invoke a Law you do not prove it, it is simply postulated on the basis of many experiments. If you were allowed one new law per observed phenomenon, anyone can do it—for each phenomenon you invoke a law that says it happens the way it does! So the real test of a Law is that it can explain many things.
This is of course the case for Newton: his Laws of Motion and Gravitation explain a huge number of things besides planetary motion: the falling apple, the Moon, the tides, binary stars, galaxy formation, and all mechanical phenomena including rocket trips to the Moon and back and every game of billiards. On the other hand, Kepler’s Laws, great though they are, are not Laws in this sense, for they do not explain other things. You can get Kepler from Newton but not vice versa. They were Laws when he wrote them down, since they could not be derived at that time, but they should perhaps not be called Laws after Newton derived them. This is, however, not an uncommon tradition. For example, even though we now know that Newton’s Law of Gravity can be derived from Einstein’s General Theory of Relativity, we still refer to it as Newton’s Law.
As I confessed, I chose this example because the phenomena are easy to visualize. I repeat that it is far from typical: people do not collect data for forty years before writing something up (not if they want a job, tenure, or funding), something as big as our solar system just comes along only once in human history as a virgin topic for study, and no one since Newton has brought along his own laws, invented the requisite mathematics to pose the problem, and gone on to solve the mathematical equations himself. It does, however, illustrate globalization fairly accurately: Kepler was a German who worked in the observatory of the Danish nobleman, Tycho Brahe (1546–1601), and was inspired by Nikolaus Copernicus, a Pole, while Newton was English.
A more recent example that conveys another set of ideas has to do with the Raman Effect. Working in a makeshift lab in Calcutta, Chandrashekhara Venkata Raman (1888–1970, 1930 Nobel Prize) observed in February 1928 that when light of frequency f was incident on certain materials, one obtained in addition to reflected light of the same frequency f or the same color, light at a slightly different frequency f’. The importance of Raman’s discovery is this. According to quantum theory, if f and f’ are possible frequencies for light emitted by an atom or molecule, so is f’–f. While radiation at the large frequencies f and f’ can be easily detected, radiation at the difference frequency f’–f (which can be very small) cannot be so readily detected. But it can be inferred from f and f’ and this gives valuable information on the structure of the molecule. Here is an analogy. Suppose I need to weigh a baby. Rather than place the squirming baby on the scale, I get on it (the scale, not the baby), measure my weight, grab the kid and read the scale again, and from the difference of two large numbers get the baby’s weight.
That this was a discovery of the highest importance is clear from the fact that the Nobel Prize followed after a remarkably short wait of two years. (Some have had to wait decades to get that early morning phone call from Stockholm and others just do not get that call at all.)
The Raman Effect was described to make the following very important point we all take for granted: Laws of Nature do not vary with time or space.
Thus the Raman Effect, first seen in Calcutta could just as easily be seen and verified in Pasadena. It was seen in 1926, but it can also be seen and exploited today. Newton’s Laws are just as good today as they were then and will continue to govern the motion of planets for all time. If a new planet is found, its orbit size and time period will have the same value of T2/R3 as the Earth. The highest possible velocity for anybody is that of light. This speed limit is universal and true not just in all countries but all over the universe. The constancy of the Laws of Nature over space and time is what makes it possible for humans, who have inhabited a very small part of the universe for a very short amount of cosmic time to make predictions that apply everywhere and for all time (even close to the Big Bang.) The constancy over space and time of Natural Laws, a great boon to us, is however a belief that has great empirical support, but not a logical necessity.
There is another piece of luck in our favor. The fact that the Laws of Nature are the same all over the universe only means that if I take an electron and proton and form a hydrogen atom here in New Haven, I will get the same atom as I would if I take that electron and proton to a lab half way around the globe or to a different solar system and let them combine there. By “same” above I mean the atom will have exactly the same characteristics: in chemical reactions, in the frequencies of light it will emit or absorb, etc. But what if creatures in another solar system built a collider that makes particles out of energy, took an electron and a proton produced by that collider and made a hydrogen atom from them? Will that hydrogen atom be the same as the one produced using an electron and proton from the Earth? The answer is yes: protons and electrons (and particles like them) are the same all over the universe and will combine to form identical atoms everywhere and all times. Protons on Earth are identical to protons anywhere else. There is not the slightest difference between two protons in mass, charge, or the forces of interaction with other particles. Though “identical” twins are never identical and “identical” cars don’t run the same way, at the basic level particles (and the atoms they form) are identical. This is due to quantum mechanics, which does not allow continuous variations in properties: either two particles are identical or they are not, there is no grey area. If you brought me an imposter electron that differed ever so slightly from the real electron, it will be exposed very clearly in a quantum experiment. For example, it will not obey the Pauli Exclusion Principle that prevents two identical fermions like electrons from occupying the same orbital in an atom. The fake electron will reveal itself by occupying the same orbital as an electron. Quantum mechanics also ensures that when the proton and electron combine to form hydrogen, only certain discrete energy levels are possible, i.e., only certain discrete frequencies of light that can be emitted or absorbed by the atom. So confident are we in this uniformity of atoms that when we see light from a distant galaxy with a wavelength that is shifted from the 21 cm wavelength of terrestrial hydrogen, we do not infer that the hydrogen there is different from hydrogen here, but that the galaxy is moving away from us and this motion causes the Doppler shift. Furthermore we use the shift to infer the galactic velocity. This is how Edwin Hubble (1889–1953) showed the universe was expanding.
Thanks to the universality of natural laws and natural phenomena, physicists in India and Japan and Poland are all seeking the same laws and exploring the same phenomena as physicists in Greenland or Iceland. This naturally fosters the exchange of ideas since we are solving the same puzzle. That we speak different languages is irrelevant, the laws of Nature are written in the universal language of mathematics. This is not all. One day, when we connect with aliens, they too will share their findings on this same quest and the “globe” in globalization will refer, not to our Earth, but to the closed and finite universe we live in.
In manifesting herself to one and all in the same fashion, Nature also serves as the ultimate arbiter of scientific disputes and the correctness of theories. If the experiments are against you, you lose, no matter who you are, and conversely, if they support you, you win regardless of who you are.
The preceding statement is true in the long run, but not in the short term. Personalities and prestige can cloud the issue in the interim. A well-known example is that of the astrophysicist Subramanian Chandrasekhar (1910–1995, 1983 Nobel Prize), nephew of C.V. Raman who we encountered earlier. As a young doctoral student at Cambridge, Chandrasekhar had deduced that certain types of stars, called white dwarfs, could not have a mass more than roughly 1.44 solar masses (the Chandrasekhar limit). If they exceeded this mass, they would undergo collapse under the pull of gravity. The collapse of a star exceeding the Chandrasekhar limit was a precursor to the idea of black holes.
When he presented his results in 1935 to the Royal Society, Britain’s most celebrated astronomer, Arthur Eddington (1882–1944) took violent objection on the grounds that Chandrasekhar had wrongly used quantum mechanics and that his proposed behavior for a star was simply absurd. Many physicists knew Eddington’s argument to be incorrect, but did not come out in Chandrasekhar’s defense—some thought it obvious, and some were afraid to contradict Eddington. Chandrasekhar left England (where all doors were closed to him in view of the above) and migrated to the USA to become one of the most influential and respected astrophysicists in the world. His results came to be universally accepted and he won the Nobel Prize in 1983, over 50 years after his great discovery.
Theorists do not always follow experimenters by explaining what has been measured. Sometimes theorists anticipate or predict a phenomenon (say a new particle) before it is observed. I choose two examples that also illustrate generosity and globalization.
The first has to do with Einstein’s prediction in 1915, based on his General Theory of Relativity, which will be briefly reviewed. Let us recall that normally we cannot see an object that is behind an obstacle since light from the object travels in straight lines and is blocked by the obstacle. Suppose there is a star behind the Sun. We cannot see it for two reasons: the Sun is so bright you cannot see the star even if it were next to it instead of behind it. Suppose we wait for a total eclipse. We still do not expect to see a star if it is hidden. Here is where Einstein’s theory predicts that we can see some stars behind the Sun because the light they emit gets bent as it passes near the Sun and reaches our eyes. Shortly thereafter began the First World War in which England and Germany were adversaries. Though Einstein was born a German, his prediction was confirmed on May 29, 1919, by a British expedition to a total solar eclipse in an island near Africa led by none other than the same Eddington (who appeared in poor light in the last anecdote). This was a fine example of the brotherhood of scientists united by a purpose higher than the barriers erected by warring nations.
The second example begins with the Indian physicist, Satyendra Nath Bose (1894–1974) who was trying to understand how particles of light called photons that were trapped in an enclosure shared their total energy among themselves. Unlike electrons, which are fermions and obey the exclusion principle, photons are bosons: not only are they not averse to doing what the other bosons are doing, they like to mimic each other and copy the activity of other bosons. Using statistical methods that took all this into account, Bose found an answer in 1920 that he sent to Einstein, asking him if he could help him get it published. Einstein realized the merits of the paper, translated it, and had it published. A few years later Einstein realized that the method applies not only to photons but to many other bosons like He4 atoms. (Of course the name boson derives from our protagonist.) He also realized that below a certain temperature, a collection of bosons would condense: a finite fraction of the bosons in the box would all be in the same quantum state, producing some dramatic effects. This predicted Bose-Einstein condensation was finally confirmed nearly 80 years later by two Americans, Eric Cornell and Carl Weiman, and a German, Wolfgang Ketterle, who shared the Nobel Prize in 2001.
After this lengthy introduction to our profession, I dedicate the rest of the article to the question of communications in recent times.
It should be no surprise that the means by which physicists communicate with each other has evolved over the centuries. In the time of Copernicus, Newton, or Galileo, years of work were summarized in huge tomes published either by the author, a society, or by some rich patron. Copernicus published his work in six volumes under the title On the Revolutions of the Heavenly Spheres, Newton wrote his Principia, and Galileo his Dialogues concerning the two chief world systems.
This leisurely pace became inadequate as time went by due to the exponential growth of knowledge: as the saying goes, the greater the sphere of knowledge the larger its contact with the area of darkness. We have seen that by the time we came to Einstein or Bose, communication was taking place via journals. In a period of rapidly evolving developments, publication in a journal is the author’s way of establishing his priority.
One might think that with Nature being a fair arbiter and an equal opportunity employer of physicists, the publication world would be a level playing field for one and all. This was certainly not the case a few decades ago due to a problem that began to seriously affect Third World countries. I would now like to describe the problem and elaborate on a marvelous solution based on the web.
To appreciate the problem and the innovation that solved it, one must understand how physicists operated in the postwar era. Typically someone does an experiment that yields an interesting or unexpected result. For example, in the case of superconductivity one finds that as the wire is cooled down, the electrical resistance drops gradually and then suddenly plunges to zero, meaning a current can flow without a voltage to drive it! This result is then sent to a journal, refereed by peers, and eventually published. It is then reproduced in other laboratories. Meanwhile, theories are espoused to explain what is going on in the wire. Each conjecture is sent to some journal, refereed, and then published. Sometimes the answer to the research questions come in one fell swoop from one source, and in other cases (e.g., superconductivity) they take several decades to fall into place, and come from multiple authors, theorists, and experimentalists, dispersed the world over.
It is in this process of iterative and interactive progress that scientists in the Third World became seriously disadvantaged as the pace of research picked up, starting in the 1960s. First of all, they got copies of the journals months after they were published. These were typically accessed through libraries. If someone had an incisive response to what was published, they could submit it to a journal. The refereeing (with all its back-and-forth exchanges) took some more months since it was performed by regular mail. Eventually, the journal carried the paper. But the author had to pray that his colleagues in the West had not had the same idea in the intervening months. Matters became worse a few decades ago, when the custom of sending out preprints began in the West. Preprints were non-refereed previews of the works circulated by the authors to a few chosen colleagues. If you were not in the club, you were not privy to this information and had to wait for it to appear in print, while those in the club had prior access. Even if you were in the club, but lived in the Third World, it took time to receive the preprints by sea mail. If you sent your own preprints (on what looked like recycled toilet paper) they just did not carry the same authority as the glossy and beautifully typeset or laser-printed equivalents from the West.
That was the problem, now here is the solution.
Our story has two parts, one well known to the general public and the other the focus of this essay.
The first concerns Tim Berners-Lee, who was working at CERN, The European Center for Nuclear Research. CERN currently houses the Large Hardron Collider and has been a focal point for international collaborations on huge accelerator based projects in elementary particle physics for decades, involving teams with more than a thousand members. Berners-Lee had the idea of a website in which members could share their results and data. The first website opened on August 6, 1991. The underlying protocol was simply given away by Berners-Lee and we all know how the web has evolved today to dominate so many aspects of our lives. I will turn to the part that affected physicists.
In 1991, Paul Ginsparg, a string theorist at the Los Alamos National Lab, set up a website (xxx.lanl.gov) where authors could upload their papers to his machine electronically. (There is a story within the story of the upload involving what is called TeX. I will come to it shortly.) The machine keeps track of each article as it arrives. The next morning readers all over the world will see the abstracts of all papers submitted in the last 24 hours. If their interest is aroused, they can download the whole paper to be read or printed out and filed. The author remains free to submit the article to a regular journal, and if the paper is published elsewhere, indicate so on Ginsparg’s machine. This system has been in place for nearly two decades now. Ginsparg wrote the entire program on his own, without funding, in his spare time. It was nothing short of visionary thinking, and nothing short of brilliant to execute it and set up machinery that has never crashed as far as I know. Of course now he heads a much bigger operation at Cornell with a lot of well deserved support. The site is now called http://arxiv.org and handles papers from many sub disciplines.
As long as you have access to the Internet, you can search the electronic archive and dig up any paper back to 1991. From any one paper, you can follow the trail to yet another with the same ease. For scholars who in years past spent hours sifting through moldy library volumes, this is an incredible advance! There is no question of a missing volume, no question of the one issue you care about having “gone to the binders” or been borrowed by the Head of the Department on an indefinite loan, looking for a journal your institution does not carry, or not knowing which journal the article appeared in. There is also no danger of publishing a paper and then finding out that the same results appeared in a journal you do not read or of which you were not aware. By the same token, you cannot rightly claim that you did not know that someone had anticipated your latest work. Nowadays, in just about any area of physics the number of people who do not read the archived papers online is very small—and rapidly shrinking.
Ginsparg’s system is a great equalizer. Consider some physicist from the Third World. He no longer has to wait four to six months before he gets the copy of the new papers. If he has a response, he does not have to wait another four to six months (possibly longer, if referees have questions) to get that response published. This debilitating delay of nearly a year (which can be a kiss of death in today’s fast-paced environment) is completely wiped out in the electronic version. The “inner circle” of people on the preprint list exists no more, and this applies not just to the Third World but to every sort of club that excluded anyone. As for the appearance of the paper, the situation is completely reversed: the paper from the West is printed by the Third World user on Third World paper with a Third World printer and vice versa! Some of these considerations also apply to physicists in lesser-known universities in the West. In the electronic archive, as seen on the computer screen, all articles look the same; all are treated the same way and all take the same time to see the light of day, i.e., less than a day. There was a time when you had to choose between paying huge page charges and having your paper face further delays. Publishing on the network costs nothing. There is also no danger of a referee stealing your ideas while blocking the publication of your paper.
Now for the story within the story. Ginsparg’s idea of a worldwide archive to which everyone could upload their papers on an equal basis runs into a serious snag stemming from the fact that the physics papers are generally filled with foreign characters and complicated mathematical expressions. Clearly one needs some kind of software to produce these formulas. This is where the problem comes in.
Consider Equation (5) from this article:
T2/R3 = (4?2/GM) (5)
which I typeset using Microsoft Word since the rest of article was easier to compose in Word. Suppose this equation were a part of a paper I am trying to upload to the archive. If I upload in the Word format I need to make sure my readers can all view it. What if they do not have this version of Word? What if I use an exotic mathematical software designed for equations involving exotic fonts? The equations may look beautiful on my computer, but illegible to readers who do not have my program. Here is where Ginsparg turned to the system invented by Donald Knuth, a computer science professor at Stanford. Knuth invented a program called TeX. In this scheme the production of papers has two parts. In the first—the so-called the raw file—you use only ASCII characters (essentially the alphabet, numbers, and a few others), which are supported by even the most primitive computer. Then comes the formula. Equation (5) above would be inserted thus:
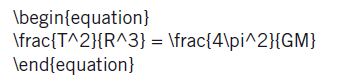
(Do not worry if this makes no sense: I will decode it later.) Then you download the (free) TeX program. When you run it, it asks for your raw ASCII file, producing an output as a Postscript or PDF file in which our equation miraculously appears as follows:
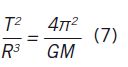
The TeX program has all the fonts you need for mathematical expressions and characters. It takes care of typesetting fractions and fractions within fractions, boldface, equation numbering, and so on.
To forward the file to another person or upload it to the archive, you have the choice of either sending the TeXed version in a PDF format (easily done with today’s huge bandwidths) or, as was more common in the past, just the ASCII file, which can be downloaded and TeXed at the other end using the free program.
Just for fun, let us see how the computer knows your intentions for Equation (5). Clearly, begin{equation} is the signal used to initiate an equation. In the next line frac indicates you want a fraction. Every fraction command is followed by two closed curly brackets {..} that contain the numerator and denominator respectively. Notice how pi stands for ?.. end{equation} signals a return to regular text.
Now it is true that if you want to play this game, you need to learn TeX. But it is quite intuitive and most people master it without difficulty. Most importantly, it is in your control, unlike software and bandwidth. It is also a nice language to use in email if you are describing some equation. For example you might say to a friend “Suppose G_{mu nu}= 16 pi T_{mu nu}…” and the reader knows you mean:
![]()
Additionally, TeX also has a simple way of embedding any graph or chart.
Paul Ginsparg was honored with a MacArthur Prize in 2001. The revolution he initiated in a corner of particle physics has since spread to many sister disciplines. Since the site is not refereed (although there is some broad policing), you can publish anything you want. But remember that if you make a fool of yourself too often, you will lose credibility. It is common to send the papers from the archive to refereed journals both to get valuable input and build your reputation towards tenure. The delays in this process are no longer pernicious as they used to be, since your work is already “out there.”
I want to close with another Internet revolution that helps with science education at a lower level. This pertains to entire courses that are now available on the web. I had the opportunity to take part in one such experiment a couple of years ago. If you go to http://oyc.yale.edu/physics you can access my lectures on Introductory Physics from the fall of 2006. (Yale used a grant from the Hewlett Foundation to pay for the production costs.) You will have access to the lectures (video and audio), the audio transcript, problem sets, their solutions, exams, and their solutions. This is absolutely free and available to anyone on the planet. I am aware of many institutions around the world which use these as a basis for a course, of students from universities in the US and abroad using this for self-study and for supplementing their regular classes. This is, of course, not the only course Yale has made available, and Yale is not the only institution to share its resources in this way. Many institutions around the world have done so. Many years ago when I was an engineering student in India teaching myself physics, I would have loved to have access to this kind of material. I am glad the current generation is better positioned to get at this information.
This concludes my essay with its rather idiosyncratic choice of topics and examples and of characters whose lives were intertwined in curious ways: Raman was Chandrasekhar’s uncle, Eddington attacked Chandrasekhar wrongly, but courageously verified Einstein’s theory, Einstein helped Bose publish his work and extended it, and Cornell, Ketterle, and Wieman demonstrated Bose-Einstein condensation.
Acknowledgements
I take this opportunity to thank Nayan Chanda, the Director of Publications and the Editor of Yale Global Online Magazine at the Yale Center for the Study of Globalization for inviting me a few years ago to write a short piece for Yale Global on which this essay is based.
Notes
- It is said of the great theorist Wolfgang Pauli (1900–1958, 1945 Nobel Prize) that the mere passage of a train carrying him through a town coincided with an explosion in a local physics lab.
Comments on this publication