In 1619, mathematician Henry Savile, a patron of Oxford University, interviewed fellow scholar Edmund Gunter as a candidate for the new chair of geometry. Gunter arrived with his astronomical quadrant and compass in hand and began showing Savile how he could calculate the position of the stars or the distance between churches. Savile dismissed him with a stinging rebuke, asserting that this was not geometry but a “mere showing of tricks.” It was once common for mathematicians themselves to disregard the practical applications of their subject. But although mathematics has always found uses, nowadays it is the cornerstone of our digital age; even something as everyday as, for example, watching a streamed movie from our armchair can be derived from abstruse mathematical theories.
In Spain, the Princess of Asturias Foundation has awarded its Scientific and Technical Research Prize in 2020 to four mathematicians: Yves Meyer, Ingrid Daubechies, Terence Tao and Emmanuel Candès, for their “immeasurable and ground-breaking contributions to modern theories and techniques of mathematical data and signal processing.” According to the jury’s decision, the contributions of the award-winners have been key in the development of various digital technologies, especially from two related fields: the theory of wavelets and the techniques of compressed sensing and matrix completion.

Wavelets were developed as a mathematical instrument in the 1970s by Jean Morlet and Alex Grossmann. Any signal, like an image, can be represented by a complex curve with sharp rises and falls. That signal can be broken down into a set of simpler, brief oscillations, which are born and die at specific frequencies. Thus, these wavelets allow a representation of the signal that permits the original information to be recovered more accurately than another classical mathematical instrument called a Fourier transform. From the 1980s onwards, the work of Belgian physicist and mathematician Daubechies —whose doctoral thesis was co-directed by Grossmann— and Meyer, from France, pioneered the development of wavelets of various shapes and sizes.
Image compression and recovery of damaged parts
Wavelets permit the use of compression algorithms that can process and interpret signals with little loss, eliminating background noise and even recovering damaged parts of the original information through an operation called deconvolution. In the first decade of this century, the Australian-American Tao and French mathematician Candès developed the techniques of compressed sensing, compressive sampling and matrix completion, which allow signals to be reconstructed with high fidelity from scattered data packages obtained by partial measurements. This mathematical trick to get more for less means a savings of resources at all levels: from collecting a sample, digitizing it and storing the data, to transmitting and decoding it.
These technologies have a wide range of applications on our digital planet, which is crisscrossed by billions of pieces of data at any given moment. As Peregrina Quintela, professor of Applied Mathematics at the University of Santiago de Compostela and member of the jury that has awarded the four researchers, explains to OpenMind: “They provide data compression techniques (they can be photos, images, signals) that, starting from a very high resolution image, are compressed and saved in low resolution (thereby taking up few megabytes), and when it is retrieved it is decompressed and returns to high resolution without loss of sharpness with respect to the original image or signal.” As an example, Daubechies wavelets were used for the development of the JPEG image compression standard launched in 2000.

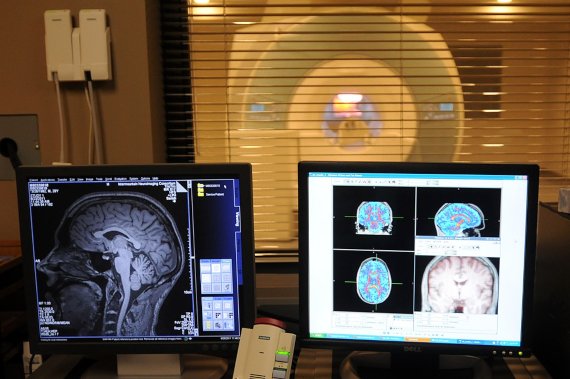
Similarly, these mathematics allow digital platforms such as Netflix, HBO and others to send movies and series to our devices on demand, in the highest resolution and without the need to download large files. But this is only the tip of the iceberg. According to Quintela, this “exceptional example of the integration of theoretical results of mathematics, which we would call more basic, with tools applied to information processing,” also has enormous scientific utility, such as the processing of images from the Hubble space telescope or the signals from gravitational waves in the LIGO experiment, and medical uses, in Magnetic Resonance Imaging (MRI) equipment.
A great versatility of technological applications
The latter is the most prominent application of the work of Terence Tao, a mathematical genius since childhood and the youngest professor ever appointed to such a position at the University of California, Los Angeles. “My compressed sensing work with Candès has been used to reduce the scanning times of the newest generation of MRI machines, which is particularly important when scanning children as in the past they sometimes needed to be anesthetized in order to remain still enough for the duration of the MRI scan,” the award-winning mathematician explains to OpenMind.
Proof of the great versatility of these technologies is provided by another example cited by Tao, which is also related to Netflix, although in a very different aspect: “My matrix completion work with Candès has been used to improve predictions for consumer ratings of products,” he explains. This use was exploited in the competition Netflix launched from 2007 to 2009 to design new tools to improve movie recommendations to its customers, a feature that the streaming video platform has identified as one of the strengths of its service.
Although current prediction algorithms use other different systems, it is undoubtedly an indication that these fields of mathematics are still brimming with application possibilities. “At one point there was some theoretical possibility that my work with Candès could be applied to generate ultra-high broadband wireless internet,” says Tao. For her part, Quintela points out some potential future avenues for this technology: “It would facilitate the collaborative work of surgeons if this technique were combined with artificial vision in streaming; in aeronautics it improves the processing of images and signals in real time in flight, making air navigation or the piloting of drones even easier and safer.”
Nevertheless, Quintela stresses, it is likely that many future uses are still unsuspected today: “We are living through a real digital revolution in which findings like those of these researchers can be a source of inspiration.” As mathematician Peter Rowlett wrote in Nature, a wonderful quality of mathematics is that it can offer answers to questions that have not even been asked yet, and may not be asked for decades to come, or even centuries. Or perhaps never. According to Rowlett, “there is no way to guarantee in advance what pure mathematics will later find application. He continues: “This extension and abstraction without apparent direction or purpose is fundamental to the discipline. Applicability is not the reason we work, and plenty that is not applicable contributes to the beauty and magnificence of our subject.”
Comments on this publication