Until the end of the nineteenth century no mathematician had managed to describe the infinite, beyond the idea that it is an absolutely unattainable value. Georg Cantor was the first to fully address such an abstract concept, and he did it by developing set theory, which led him to the surprising conclusion that there are infinities of different sizes. Faced with the rejection of his counterintuitive ideas, Cantor doubted himself and suffered successive nervous breakdowns, until dying interned in a sanatorium. Nowadays, mathematics cannot be understood without his revolutionary insights.

Although he was born in St. Petersburg (Russia), where his parents had emigrated from Denmark, Georg Cantor (3 March 1845-6 January 1918) spent most of his life in Germany. The infinite interested him from a young age, and in his thirties he published the articles that developed his set theory, in which he formalised various ideas about mathematical infinity. For Cantor, sets are collections of objects that can have finite or infinite elements. For example, the set of fingers of a hand has finite elements ({thumb, index, middle, ring and pinky}), while the set of natural numbers (N = {0, 1, 2, 3, 4, 5, 6…}) has infinite elements. Cantor established the concept of cardinal as the number of elements that a set has: following the same example, the cardinal of the set of fingers of one hand is five (5) and the cardinal of the set of natural numbers is infinite (∞). His colleague Richard Dedekind, with whom he corresponded for years, had already considered infinite sets in 1872, but Cantor also realised that not all infinite sets are of the same size. In other words, there are infinite sets that have different cardinals.
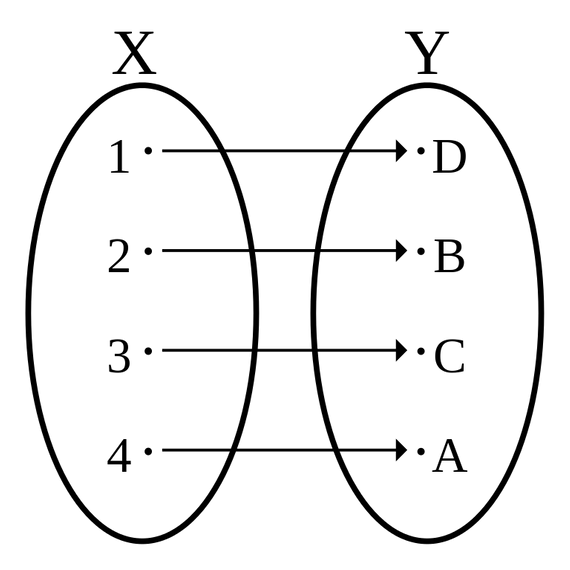
Bijective functions
It would seem that the set of natural numbers (N = {0, 1, 2, 3, 4, 5, 6…}) comprises more elements than the subset containing prime numbers (P = {2, 3, 5, 7, 11, 13…}). However, Cantor showed that both have the same cardinal, and therefore the same infinite number of elements. To demonstrate this, he paired each of the elements that form a set with the elements of the other, which is known as establishing a bijective function (or one-to-one correspondence) between both sets. In the case of natural numbers and primes the pairing could be 0-2, 1-3, 2-5, 3-7, 4-11, 5-13…
On the contrary, in one of his most famous demonstrations, Cantor proved that it was impossible to establish a bijective function between the set of natural numbers and the set of points that form a number line. He thus came to the conclusion that the cardinal of the set of real numbers was greater than that of natural numbers: they were infinities of different sizes. He demonstrated even more, that the infinite cardinal of the real numbers is followed by another greater one, and this in turn is followed by an even greater one, and so on. To the smallest of all these infinite cardinals, the cardinal of natural numbers, he called it aleph-zero (aleph is the first letter of the Hebrew alphabet). The next ones he called aleph-one, aleph-two, aleph-three, etc. All these cardinals of infinite sets are known by the name of transfinite cardinals.

Some of the results of set theory were really surprising and counterintuitive, the reason why Cantor asked Dedekind on more than one occasion to review his proofs. He also had to invest a lot of effort in convincing other more sceptical math colleagues. As a result of his discoveries, Cantor ended up developing a complete transfinite arithmetic, which equated the operations of addition and multiplication of natural numbers with the infinite cardinals that he defined. Each natural number can be identified with the cardinal of a finite set. As we said, 5 can be identified with the cardinal of the set of fingers of one hand. Thus, Cantor defines the operations of addition and multiplication of numbers as if they were operations between the cardinals of sets, whether finite or infinite.
The beginning of nervous breakdowns
Both Cantor and Dedekind were exceptional mathematicians in their time, but neither ever obtained a prominent professional position. While Cantor remained at the University of Halle, a small institution, for most of his life, Dedekind never went beyond being a high school teacher in his hometown of Brunswick. The main detractor of Cantor was Leopold Kronecker, who prevented him from entering the prestigious University of Berlin every time he tried. Kronecker argued that mathematics should be based on whole numbers, and systematically rejected that incipient new branch of mathematics. Kronecker’s attacks ended up provoking in 1884 the first of Cantor’s nervous breakdowns, which he suffered periodically for the rest of his life.

Cantor spent the end of his days in a psychiatric hospital in Halle, where he died. However, his set theory ended up becoming the common language used in the various branches of modern mathematics. A few years after his death, the renowned mathematician David Hilbert said that transfinite arithmetic is “the finest product of mathematical genius and one of the supreme achievements of purely intellectual human activity.”
Comments on this publication