Tras el frenazo intelectual que supuso la Edad Media para Occidente, en el siglo XVII Europa vivió un renacimiento matemático con epicentro en Francia. En ese resurgir de conocimiento sobresalió Descartes, que como buen filósofo se atrevió a cuestionar los pensamientos científicos predominantes y apostó por la razón, la experimentación y la observación frente a la tradición y la autoridad. Suya es la célebre frase “Pienso, luego existo”. Con esa idea escribió el Discurso del método para conducir bien la propia razón y buscar la verdad en las ciencias, un tratado filosófico en el que además desarrolló la geometría analítica o cartesiana, uno de los filones más ricos del pensamiento matemático.

Desde la época de Platón, más de 2000 años atrás, no se había dado una comunicación tan intensa entre matemáticos como la que comenzó en Francia a partir del segundo tercio del siglo XVII. Entre los protagonistas de este intercambio postal de ideas se encontraba René Descartes (31 de marzo de 1596 — 11 de febrero de 1650). Nacido en La Haye, un pueblo del centro de Francia, Descartes fue un niño enfermizo al que obligaban a pasar las mañanas en la cama, tiempo que invertía en leer y estudiar. Con 20 años se trasladó a París, donde entró en contacto con otros intelectuales de la época y comenzó a profundizar en una de las disciplinas científicas en las que destacaría: las matemáticas. En 1628 se mudó de forma definitiva a Holanda en busca de un ambiente intelectual más libre. Algo que pareció encontrar, ya que los años que pasó allí fueron los más fructíferos de su vida, cuando escribió sus obras más populares.
Un diccionario entre el álgebra y la geometría
El más famoso de los tratados de Descartes, el Discurso del método, contiene el apéndice La geometría que relaciona por primera vez nociones del álgebra con objetos geométricos, dando lugar a la aparición de la geometría analítica o cartesiana (de Cartesius, Descartes en latín). En esta nueva geometría se identifican los puntos del plano con pares de números (x,y): es un sistema de coordenadas en el que cada par nos da la posición de un punto con respecto a dos rectas perpendiculares fijadas, llamadas ejes de coordenadas. Así, cada par de coordenadas especifica un punto único del plano, y cada punto viene dado por un único par de coordenadas. Descartes había ideado una especie de diccionario entre el álgebra y la geometría, que además de asociar pares de números a puntos, le permitía describir líneas dibujadas en el plano mediante ecuaciones con dos variables —x e y—, y viceversa.
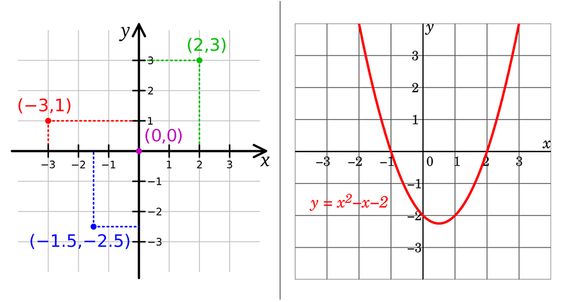
Lo novedoso de este enfoque de la geometría analítica fue que permitió resolver problemas geométricos mediante la exclusiva manipulación de expresiones algebraicas. Hasta ese momento, la geometría dominante era la euclidiana, que usaba la regla y el compás para resolver esos problemas. Y ese método de Descartes funcionó y resultó más práctico gracias que la geometría analítica representa el conjunto de soluciones de una ecuación de dos variables, x e y, mediante una línea en el plano. Por ejemplo, una ecuación del tipo ax+by=c —como por ejemplo 2x+3y=0—, que es una ecuación polinómica de grado 1, tiene como conjunto de soluciones una línea recta, que surge de unir todos los puntos con coordenadas x e y cuyos valores satisfacen esa igualdad. Las circunferencias y el resto de cónicas se representan con ecuaciones polinómicas de grado 2. Un ejemplo es la circunferencia, x2 + y2 = 4, y otro la hipérbola, xy = 1. Gracias al trabajo de Descartes, toda la geometría antigua se tradujo al estudio de las relaciones que existen entre polinomios de grados 1 y 2 —algo que hoy en día se sigue estudiando en las matemáticas de educación secundaria.
El reto a Fermat
De las relaciones que Descartes estableció con otros matemáticos franceses, ninguna fue tan intensa como la que tuvo con Pierre de Fermat, que también realizó importantes contribuciones a la geometría analítica. Fermat había desarrollado una manera de obtener la línea tangente a una curva en cualquiera de sus puntos, pero Descartes creía que aquello no era un auténtico método, así que decidió retar a Fermat —algo relativamente común entre los intelectuales de la época— a que encontrase la tangente en un punto cualquiera de la curva que tiene por ecuación x3 + y3 – 3axy = 0, hoy conocida como el Folium de Descartes. Fermat resolvió el problema, dejando en evidencia a Descartes y demostrando el éxito de su procedimiento. Un método que sentó las bases para que Newton y Leibniz desarrollasen el cálculo infinitesimal.

Aunque el mayor logro de Descartes fue el desarrollo de su geometría, también hizo importantes aportaciones en otros campos. En el de la óptica introdujo la llamada ley de refracción, que permite calcular el ángulo de refracción de la luz al atravesar la superficie que separa dos medios con índice de refracción distinto (por ejemplo, el aire y el agua). También en física, Descartes estableció que el movimiento rectilíneo es el natural, en contra de la idea del momento que aseguraba que era el circular uniforme, como revelaba el movimiento de las estrellas y de los planetas.

Hoy en día, Descartes es considerado no solo un filósofo ilustre, sino también un destacado matemático y físico. Murió de una neumonía en Estocolmo, solo un año después de acudir invitado por la reina Cristina para formar parte de la corte sueca. Tras un largo periplo, no exento de controversias, sus restos regresaron a Francia. En la actualidad es posible contemplar en el Musée de l’Homme de París su cráneo. Aquel que albergó una de las mayores revoluciones matemáticas de la historia.
Comentarios sobre esta publicación