La revolución matemática gestada por Newton en su granja mientras se recluía de la peste bubónica hizo que la figura del matemático pasase a ser considerada fundamental por las sociedades y cortes europeas del siglo XVIII. Los expertos en la materia evolucionaron de simples aficionados a los números a ser respetados profesionales capaces de resolver problemas prácticos de lo más diversos, desde arquitectónicos o sociales hasta balísticos y navales.
Las grandes potencias se disputaban los servicios de los mejores matemáticos, reservándoles muchas veces el papel de asesores de sus máximos dirigentes. Y, sin lugar a duda, el matemático más respetado e importante del momento –y de los más importantes de toda la historia– era el suizo Leonhard Euler, quien desarrolló la mayor parte de su carrera profesional en las cortes de Prusia y Rusia, al servicio de Federico II el Grande y Catalina la Grande, respectivamente.
Entre los problemas prácticos más importantes resueltos por Euler destacan el de la predicción de las fases de la luna en fechas lejanas, una información básica para la elaboración de tablas para la navegación oceánica, y el desarrollo del método algorítmico, desde entonces una herramienta fundamental para los matemáticos y que se sigue utilizando actualmente en campos como la física, la química o la economía.
No obstante, el problema más famoso en el que se vio envuelto Euler y que contribuyó a popularizar su figura fue el conocido como problema de los puentes de Königsberg, en referencia a la antigua ciudad prusiana que posteriormente se transformó en la rusa Kaliningrado. Este problema fue el punto de partida para que Euler terminase por desarrollar algunos de sus teoremas más importantes.
Juego 1
Conecta todas las islas del diagrama entre sí siguiendo las siguientes reglas:
- El número dentro de cada isla indica cuantos puentes están conectados a ella.
- Cada par de islas solo puede estar conectado entre sí por dos puentes como máximo.
- Los puentes solo pueden conectar islas en líneas rectas no diagonales, tienen que empezar y acabar en una isla y no puede cruzarse entre ellos.
Ejemplo:


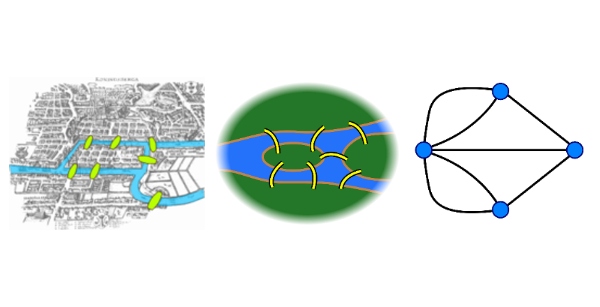
Construida sobre los bancos de arena del río Pregolia, la ciudad constaba de cuatro barrios independientes conectados por siete puentes, que atraían a numerosos visitantes. Mucha gente se preguntaba si era posible trazar una ruta que permitiese cruzar todos los puentes sin pasar dos veces por ninguno de ellos, algo que parecía imposible y, de hecho, lo era. Euler fue el encargado de demostrarlo matemáticamente y en su empeño inventó una nueva forma de representación matemática, los grafos. Al formular el Teorema de Euler, fundó asimismo la Teoría de grafos, la rama matemática que se ocupa de su estudio.
Euler tomó el plano de la ciudad y elaboró una representación minimalista en la que cada barrio se representaba por un punto y cada puente por una línea. Es decir, la representó con un grafo.
A partir de este primer grafo, dedujo que para trazar el recorrido deseado y si el punto de partida era el mismo que el final –la ruta empezaba y acababa en el mismo barrio, conformando un circuito cerrado–, cada punto debería estar unido a un número par de líneas, ya que cada vez que el viajero atraviesa una masa de tierra debe entrar a ella por un puente y salir por otro distinto. Si por el contrario el trayecto empieza y acaba en lugares distintos entonces los barrios inicial y final pueden tener un número impar de puentes. Como en Könisberg las cuatro masas de tierra estaban unidas a un número impar de puentes era imposible trazar la ruta deseada.
Pero lo más trascendente es que a partir del grafo de Könisgberg, Euler generalizó que es posible recorrer cualquier red sin pasar dos veces por la misma línea si todos los puntos están unidos a un número par de líneas o si bien dos puntos están unidos a un número impar de líneas.
En la actualidad, la Teoría de Grafos se aplica a la resolución de problemas prácticos en numerosas disciplinas y campos: teoría de juegos, inteligencia artificial, optimización de recurso, clasificación e incluso diseño y resolución de laberintos.
Juego 2

Además, al reducir el problema a un grafo, prescindiendo de aspectos irrelevantes para la resolución del problema como la longitud o curvatura de los puentes y las dimensiones y contornos de los barrios, Euler también estableció los pilares de la topología: la rama matemática que estudia solo la esencia de los objetos, en contraposición con la geometría, que estudia la forma y tamaño exactos. La gran ventaja de la topología es que permite representar de una forma muy visible las relaciones entre distintos entes y con ello visualizar más fácilmente la mejor forma para alcanzar el resultado o solución deseada.
Una de las aplicaciones más populares y conocidas de la topología es la representación de los trayectos de las distintas líneas del transporte público: metro, autobús o ferrocarril; en la que las estaciones y vías que las conectan se representan como puntos y líneas, lo que permite al usuario identificar de un vistazo cual es el trayecto mas corto para llegar a su destino y en que estaciones debe cambiar de línea.
Juego 3

Soluciones
Miguel Barral

Comentarios sobre esta publicación