En 1867 el gran físico escocés James Clerk Maxwell presentaba a su demonio. Una criatura imaginaria que desafiaba la segunda ley de la termodinámica, considerada como inviolable. 150 años después, por fin los físicos han logrado demostrar experimentalmente que el diablillo de Maxwell tenía truco.
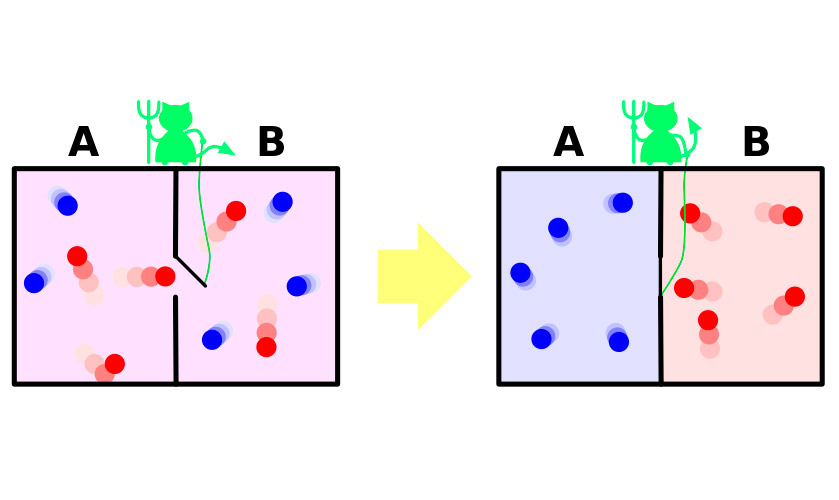
- Imaginemos un sistema cerrado (aislado), una caja llena de un gas a una determinada temperatura. Esto significa que las moléculas de dicho gas se mueven a una determinada velocidad media. Algunas moléculas se mueven más rápido que la media y otras viajan más lentamente.
- Supongamos ahora que en el interior de la caja existe una división que separa el lado derecho del izquierdo. Ambos lados de la caja estarán llenos de gas a la misma temperatura.
- Y por último imaginemos que el tabique que separa ambas partes dispone de una minúscula trampilla, que puede abrir y cerrar a voluntad una diminuta y manipuladora criatura para conseguir que las moléculas más rápidas se concentren en el lado izquierdo y las más lentas en la mitad derecha. Y por tanto, aumentaría el orden del sistema, vulnerando la Segunda ley de la Termodinámica.
El demonio de Maxwell no sólo ha servido de inspiración para generaciones de físicos. También para idear este pasatiempo que transmuta al jugador en diablillo del siguiente sistema: un tablero o cuadrícula en el que hay 18 moléculas y en el que el objetivo es introducir orden. Eso se logra colocando las moléculas en celdas, bajo las siguientes premisas:
- Cada fila y columna deben contener exactamente dos moléculas.
- Las celdas ocupadas no pueden ser contiguas (tampoco en diagonal).
- Los números que figuran en los márgenes de la cuadrícula indican el número de celdas vacías entre las dos estrellas de esa fila o columna.
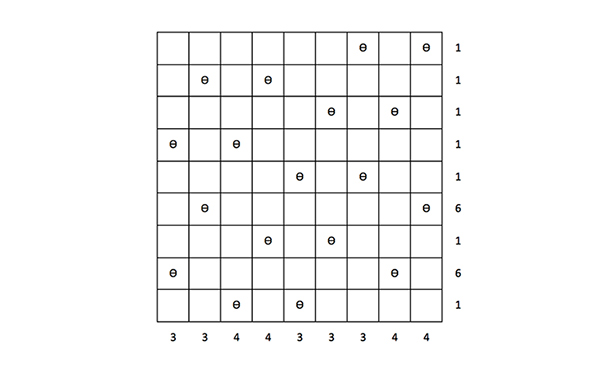
Tablero 1: para aprendices de diablillo

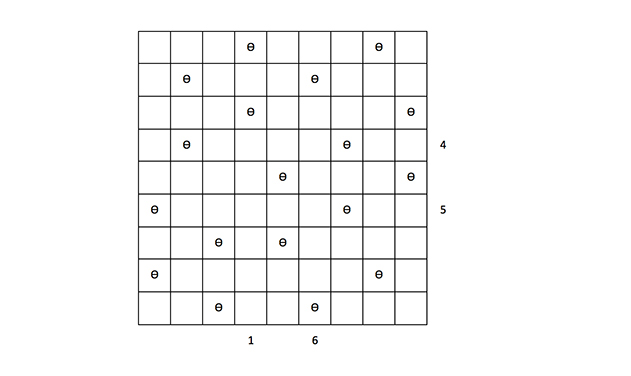
Tablero 2: Para auténticos Mefistóteles

Resolver estos dos tableros exige un notable gasto de energía mental, como el de los físicos que se afanaron en intentar resolver y desmontar la paradoja formulada en 1867 por Maxwell. Veámoslo antes de conocer la solución al rompecabezas.
En 1929, en un artículo hoy considerado como “clásico”, Leo Szilard (uno de los padres de la energía nuclear) ofrecía una primera explicación: para determinar qué moléculas son más rápidas y cuales más lentas, el diablillo necesitaba adquirir información, lo que requeriría realizar medidas. Un proceso que conllevaba un consumo de energía y un aumento de la entropía del sistema que compensaban las diabluras de la criatura.
Tres décadas después, Rolf Landauer perfilaba y perfeccionaba la explicación al matizar que el mero hecho de procesar la información, es decir, discernir cuál va más rápido y cuál más despacio conllevaba un esfuerzo mental y, por tanto, un consumo de energía por parte del cerebro. Y ese esfuerzo aumentaba la entropía o desorden del sistema. De algún modo, las neuronas quedaban “descolocadas”. Algo fácil de entender desde la experiencia personal: tras afrontar un considerable esfuerzo mental, caemos en un estado de disipación en el que cuesta volver a concentrarse en cualquier otro asunto.
Y recientemente este argumento teórico ha sido confirmado experimentalmente después de que un equipo de físicos haya creado una versión cuántica del diablillo en el laboratorio.
Comentarios sobre esta publicación