Weather is one of the large-scale examples of chaotic systems; in fact, it was weather-research that revealed what chaos really is; small perturbations in the atmosphere can cause enormous climate changes. This was discovered by the North American theoretical meteorologist, Edward Norton Lorenz (1938-2008).
The article in which he presented his results in 1963 is one of the great achievements of twentieth-century physics, although few non-meteorological scientists noticed it at the time. This was to change radically over the following decades. That change of attitude had much to do with a famous sentence that Lorenz included in a lecture he gave on December 1972 at a session of the annual meeting of the AAAS (American Association for the advancement of Science): “a butterfly flapping its wings in Brazil can produce a tornado in Texas.” Previously, Lorenz had used the example of a seagull causing a storm, but finally made it more poetic with a butterfly, following suggestions from colleagues. In 1987, the term “butterfly effect” took flight thanks to James Gleick’s best seller ‘Chaos: Making a New Science’—and Lorenz’s discovery reached a general audience.
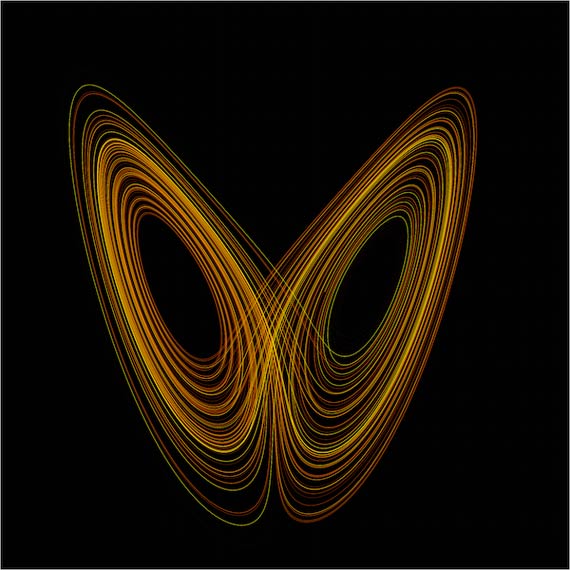
In his weather research, he developed simple mathematical models and explored their properties with the help of computers. But, in 1960, he found that something strange occurred when he repeated previous calculations. Here is how he, himself, reconstructed the events and his reaction in the book, ‘The Essence of Chaos’, which he wrote years later:
“At one point, I decided to repeat some of the calculations in order to examine what was happening in greater detail. I stopped the computer, typed in a line of numbers that had come out of the printer a little earlier, and started it back up. I went to the lobby to have a cup of coffee and came back an hour later, during which the computer had simulated about two months of weather. The numbers coming out of the printer had nothing to do with the previous ones.
I immediately thought one of the tubes had deteriorated, or that the computer had had some other sort of breakdown, which was not infrequent, but before I called the technicians, I decided to find out where the problem was, knowing that that would speed up the repairs. Instead of a sudden interruption, I found that the new values repeated the previous ones at first, but soon began to differ by one or more units in the final decimal, then in the previous one, and then the one before that. In fact, the differences doubled in size more-or-less constantly every four days until any resemblance to the original figures disappeared at some point during the second month.
That was enough for me to understand what was going on: the numbers I had typed into the computer were not exactly the original ones. They were rounded versions I had first given to the printer. The initial errors caused by rounding out the values were the cause: they constantly grew until they controlled the solution. Nowadays, we would call this chaos.”
What Lorenz observed empirically with the help of his computer, is that there are systems that can exhibit unpredictable behavior (which does not mean “not subject to laws”) in which small differences in a single variable have profound effects on the system’s later history. Weather is such a chaotic system, which is why it is so hard to predict, so unpredictable, as we often put it.
It is becoming increasingly clear that chaotic phenomena are abundant in nature. We already see them at work in the fields of economics, aerodynamics, population biology (for example, in some “predator-prey” models), thermodynamics, chemistry and, of course, in the world of biomedicine (one example is certain heart problems). It seems that they can also show up in the apparently stable movements of the planets.
> More on chaos theory, relativity and quantum physics in the essay “The world after the Revolution: Physics in the Second Half of the Twentieth Century”, by José Manuel Sánchez Ron”
Comments on this publication