In 1966, mathematician Leo Moser posed an apparently trivial issue that soon became known as the moving sofa problem: What is the sofa that offers the largest seating area and which can be pulled (but not turned upright or inclined, etc.) around a 1-meter wide hallway and with a 90° corner or turn?
This is a problem that, after more than fifty years, has not yet been satisfactorily solved —at least from a mathematical point of view, in other words, where the solution comes accompanied by a mathematical proof that is accepted as unique and impregnable. As long as this is not achieved, any solution will be a mere conjecture susceptible to be invalidated, violated and overcome at any time.
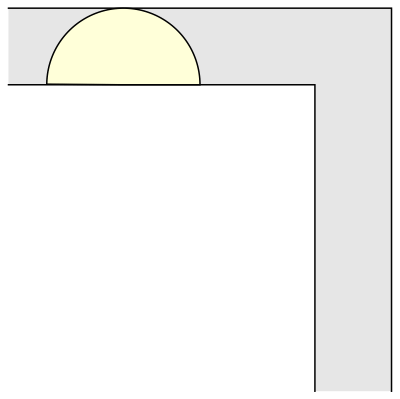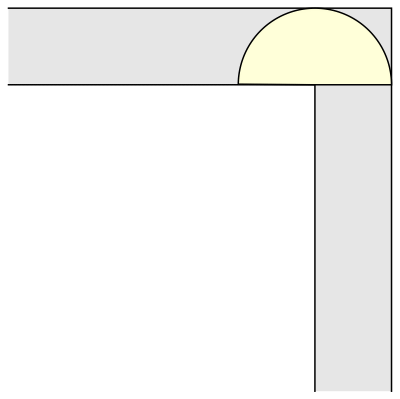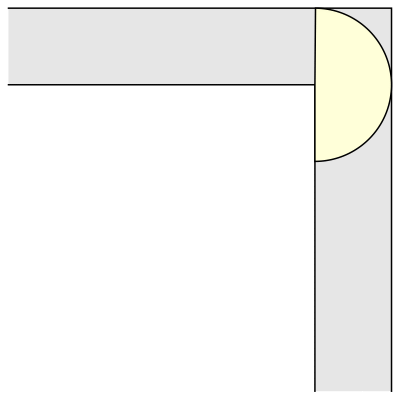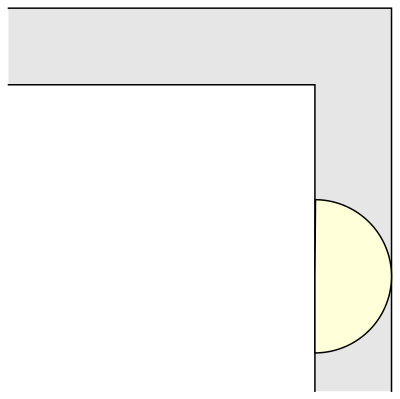The first and immediate response was that of a 1-meter wide square sofa (its surface being 1 square meter). That solution was also immediately surpassed by that of a semi-circular sofa of radius 1 (and surface π/2 = 1,57 square meters), a shape that allows for perfect rotation around the corner (always in the horizontal plane or in two dimensions).
In 1968, mathematician John Hammersley stated that a sofa shaped like a bridge or the telephone handsets of the time, with a radius = 2/π, offered a maximum area of 2/π + π/2 = 2,2074 square meters, but he did not mathematically proved how he came up with the result. That left the door open for other mathematicians to continue seeking a definitive solution or, at least, proof that Hammersley’s was the one. Over the next two decades, it was accepted that this was the optimal form. But then, in 1992, mathematician Joseph Gerver found an even better shape by rounding the inner edges and achieving a slightly larger area, of 2,2195 square meters. This is the answer that currently remains valid… although, again, it is only a conjecture in the absence of a conclusive mathematical proof.
In parallel to the original sofa problem, variants have also emerged, the most popular of which seeks to find the optimal shape for a sofa that has to move through a hallway with two right angles, one on the right and one on the left. Mathematician Dan Romik recently offered a new answer to the problem, by way of conjecture, called the “ambidextrous sofa” in an article published in Experimental Mathematics.
And while some mathematicians are struggling to solve such a problem for the greater glory of their discipline and of Ikea, here you are this “alternative sofa problem”:
In these faculties of mathematics, those who know (or are afraid) that the problem of the moving sofa has a difficult solution have opted for the middle road in order to “avoid it.” Thus, all rooms and offices are connected to each other by straight hallways. The challenge is to strategically place four sofas in four different rooms so that you can always carry one of them to any room through a straight hallway, without having to face sharp, right-angled or obtuse turns.
Faculty #1:
Faculty #2:
Answer:
Miguel Barral
@migbarral
Comments on this publication