Para este nuevo reto a los lectores de OpenMind nos inspiramos en el que en 1975 planteó el matemático Jacob E. Goodman en la revista American Mathematical Monthly: el llamado problema de las tortitas. Aunque nadie ha conseguido resolverlo aún, la mejor aproximación durante casi 30 años la dejó escrita Bill Gates, en su único artículo de investigación científica.
Nuestro pasatiempo, mucho más asequible, consiste en ordenar por tamaño las tortitas apiladas, comenzando con la más grande (abajo) y terminando con la más pequeña (arriba). Tenemos tres juegos:
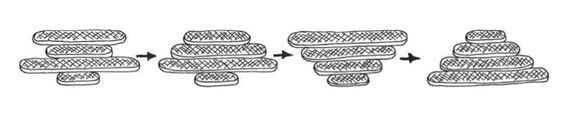
Problema 1

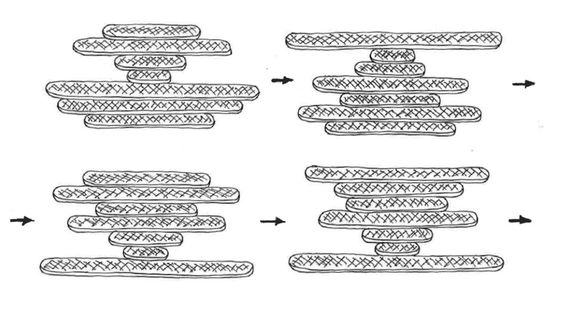
Problema 2

Problema 3

Y en los tres casos el objetivo es el mismo: hay que realizar el menor número posible de movimientos con la espátula para lograr la disposición deseada.
Cada movimiento consiste en insertar la espátula a una altura determinada de la pila, levantar con ella todas las tortitas que hay por encima y, con un rápido giro de muñeca, colocarlas volteadas en la parte superior de la pila.

El problema original
Para ayudar a resolverlo recordamos el problema original de 1975, en el que Harry Dweighter es un camarero agobiado (en inglés se dice hurried waiter, que suena casi igual) porque se encuentra con una pila de tortitas que salen desordenadas de la cocina. ¿Cuántos movimientos como máximo tiene que hacer para dejar las tortitas perfectamente ordenadas?
La pregunta cautivó de inmediato a matemáticos e informáticos. A los programadores les interesó porque podía tener aplicaciones para ayudar a reordenar datos. Y también es el tipo de problemas que apasionan a un matemático: parece muy sencillo, pero la solución se complica sobremanera según va creciendo el número de tortitas.
Si tenemos una pila de 3 tortitas, en el peor de los casos habrá que hacer 3 movimientos (es fácil comprobarlo en este vídeo); si tenemos 7 tortitas, como mucho serán 8 cambios; con 11 tortitas son 13 (aquí ya necesitamos un ordenador para calcularlo); con 19 tortitas son 22 movimientos; y con 20 tortitas, ¡ya no se sabe! Podrían ser 23, o 24, o incluso 25… Pero dada la dificultad de calcular todas las permutaciones de tortitas y estrategias de cambio, ni siquiera se ha podido demostrar la solución con la ayuda de los ordenadores más potentes actuales, tras cuatro décadas de evolución informática. Lo que sí se consiguió (y relativamente pronto) fue una fórmula que estableció el límite superior de movimientos necesarios.
El logro de Gates
En 1979 un estudio demostró que el número requerido de cambios en una pila de n tortitas siempre es menor a (5n+5)/3. Es decir, si tenemos 20 tortitas de distinto tamaño y dispuestas aleatoriamente, en el peor de los casos seguro que nunca serían necesarios más de 33 movimientos para ordenarlas al gusto de Harry Dweighter.
Los autores de dicho trabajo eran Christos H. Papadimitrou y William H. Gates. Sí, el mismo Bill Gates que ya había fundado Microsoft. Y tuvieron que pasar casi 30 años hasta que en 2008 el logro de Gates fue superado por un equipo de investigadores de la Universidad de Texas en Dallas, que establecieron ese límite superior en 18n/11: así, ya podemos asegurarle al agobiado camarero que 32 movimientos siempre serán suficientes para ordenar 20 tortitas.
El artículo de Gates y Papadimitrou incorporaba una variación todavía más retorcida del problema original, conocida como la variante de la tortita quemada, en la que intervienen tortitas que se han quemado por un lado, de modo que además de ordenarlas correctamente por tamaño también hay que colocarlas con la cara quemada hacia abajo. Pero esto lo dejamos para próximos retos.
Soluciones:


Comentarios sobre esta publicación